Προσδιορισμός της κλίσεως των στρωμάτων με τη μέθοδο των παρατάξεων.
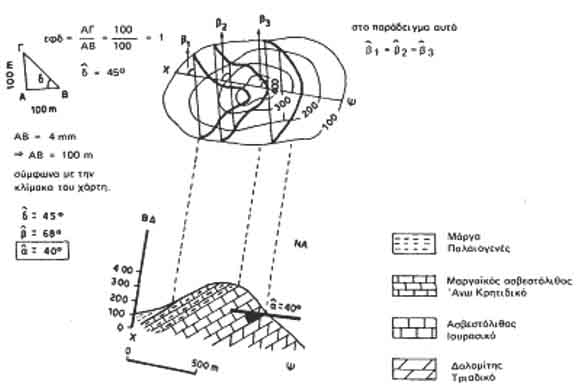 |
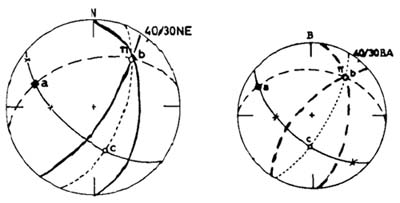
| Σχ. Κ. 13: εφα = εφδ·ημβ: Τριγωνομετρική σχέση που συνδέει μεταξύ τους τις γωνίες α,δ και β (φαινόμενη γωνία πάντοτε μικρότερη από την πραγματική). ΑΒ = προβολή στο οριζόντιο επίπεδο της απόστασης δυο παρατάξεων του γεωλογικού σχηματισμού. ΑΓ = υψομετρική απόσταση των αντίστοιχων παρατάξεων, β = γωνία μεταξύ της διεύθυνσης της τομής και της παράταξης, δ = πραγματική γωνία κλίσης (Τομή κάθετη στην παράταξη. Μια μόνο τιμή), α = φαινόμενη γωνία κλίσεως (Τομή πλάγια στην παράταξη. Άπειρες τιμές που εξαρτώνται από τη γωνία β). |
Σε περίπτωση που έχουμε διεύθυνση τομής πλάγια στην παράταξη του γεωλογικού σχηματισμού, για την κατασκευή της αντίστοιχης γεωλογικής τομής, θα πρέπει να υπολογίσουμε τη φαινόμενη γωνία κλίσεως με την οποία θα εμφανισθεί αυτός στην τομή (Σχ. Κ. 13).
Για το σκοπό αυτό υπολογίζουμε με τη μέθοδο των παρατάξεων την πραγματική γωνία κλίσεως δ του γεωλογικού σχηματισμού και στη συνέχεια με βάση τη γωνία β χρησιμοποιώντας το εικονιζόμενο νομόγραμμα (Α) υπολογίζουμε τη ζητούμενη φαινόμενη γωνία α.
Είναι φανερό ότι σε διεύθυνση τομής κάθετη στην παράταξη του γεωλογικού σχηματισμού μας χρειάζεται μόνο η πραγματική γωνία κλίσεως, την οποία υπολογίζουμε, με το γνωστό τρόπο με τη μέθοδο των παρατάξεων. Τη γωνία αυτή χρησιμοποιούμε κατευθείαν για την κατασκευή της τομής, χωρίς να λάβουμε υπ' όψη τη γωνία β, που στην προκειμένη περίπτωση είναι 90°.
Φυσικά για την κατασκευή γεωλογικών τομών είναι δυνατόν να χρησιμοποιήσουμε και τη «μέθοδο των προβολών», η οποία στηρίζεται, κυρίως, στην προβολή ορισμένων σταθερών σημείων, χωρίς τη χρήση τριγωνομετρικών τύπων.
Οι δυο αυτές μέθοδοι (μέθοδος παρατάξεων και μέθοδος προβολών) εφόσον εκτελεστούν σωστά για μια συγκεκριμένη γεωλογική τομή, θα πρέπει να καταλήγουν στο ίδιο συμπέρασμα.
Σχέσεις φαινόμενου και αληθινού πάχους σε κεκλιμένη μορφολογία
Από το φαινόμενο πάχος του γεωλογικού σχηματισμού σε κεκλιμένη μορφολογία είναι δυνατόν να υπολογίσουμε το πραγματικό πάχος, το οποίο είναι χρήσιμο για τον υπολογισμό των πραγματικών διαστάσεων του γεωλογικού σχηματισμού.
Σύμφωνα με το σχήμα Κ. 14. και τις σχέσεις (1) (2) και (3) προκύπτουν οι εξής σχέσεις:
| Φ2 = Φ1.συνγ (4) |
Φ1
=
|
Αλ = Φ1.ημβ |
|
Φ2
=
|
Αλ
=
|
|
 |
||
| Σχ. Κ.14: Σχέσεις φαινόμενου και αληθινού πάχους σε κεκλιμμένη μορφολογία. ΑΒ = Φ1 = φαινόμενο πάχος στο ύπαιθρο. ΑΓ = Αλ = αληθινό (πραγματικό) πάχος. ΑΔ = Φ2 = φαινόμενο πάχος στον γεωλογικό χάρτη. | ||
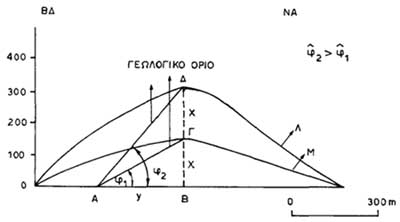
Μεταβολή της γωνίας κλίσεως ενός στρώματος όταν διογκώνεται η κλίμακα ύψους
Όταν η κλίμακα του ύψους διογκώνεται τότε στην τομή, η γωνία κλίσεως ενός γεωλογικού σχηματισμού αλλοιώνεται (πάντοτε μεγαλώνει) σύμφωνα με τον παρακάτω τρόπο.
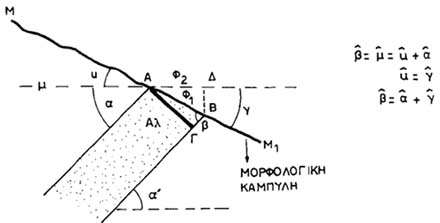
Από τα ορθογώνια τρίγωνα ΑΒΓ και ΑΒΔ έχουμε (Σχ. Κ. 15):
|
εφφ1 =
|
εφφ2 =
|
|
(1) Λ (2)
|
|
| (3) 2εφφ1 = εφφ2, ή γενικά σε ν διόγκωση |
νεφφ1 = εφφ2 |
 |
|
Σχ. Κ.15: Μεταβολή της γωνίας κλίσεως ενός στρώματος όταν διογκώνεται η κλίμακα ύψους. Μ = μορφολογική καμπύλη σε τομή με κλίμακα ύψους ίση με την κλίμακα μήκους. Λ = μορφολογική καμπύλη σε τομή με κλίμακα ύψους διπλάσια από την κλίμακα μήκους. φ1 = αληθινή γωνία κλίσεως του γεωλογικού σχηματισμού, φ2 = γωνία κλίσεως του γεωλογικού σχηματισμού σε διογκωμένη κλίμακα ύψους (διπλάσια του μήκους). |
Ένα κατεξοχήν σημαντικό μέρος μιας τεκτονικής μελέτης αποτελεί η ανάλυση της υφής (Μελέτη μορφών παραμόρφωσης και συνθηκών συμμετρίας τους, για την εξαγωγή συμπερασμάτων σχετικά με τη συμμετρία και τη διεύθυνση των τεκτονικών κινήσεων, δυνάμεων και γεγονότων που δημιούργησαν τις τεκτονικές αυτές παραμορφώσεις). Για το σκοπό αυτό, εκτός των άλλων, θα χρειασθεί ένα πλήθος μετρήσεων, (ο αριθμός τους εξαρτάται ανάλογα από το αντικείμενο της εργασίας), των επιφανειακών και γραμμικών στοιχείων της περιοχής μελέτης, (ss-επιφάνειες, s-επιφάνειες, επιφάνειες διακλάσεων και ρηγμάτων, γραμμώσεις κ.ά), που γίνονται με τη γεωλογική πυξίδα.
Η αναπαράσταση των μετρήσεων αυτών, (παράταξη, διεύθυνση κλίσης και γωνία κλίσης των επιφανειών και γραμμώσεων), με κάποιον ορισμένο τρόπο, σε διαγράμματα, καθώς και η στατιστική επεξεργασία τους, θα δώσει απάντηση σε πολλά από τα προβλήματα της ανάλυσης της υφής μιας περιοχής.
Έτσι, με τον τρόπο αυτό μπορούμε:
α) Να υπολογίσουμε τις κύριες διευθύνσεις ανάπτυξης των τεκτονικών δομών μιας
περιοχής, ώστε να κάνουμε ένα πρώτο βήμα για τον προσδιορισμό των τεκτονικών
κινήσεων και δυνάμεων που διαμόρφωσαν τις τεκτονικές αυτές δομές.
β) Να αξιολογήσουμε τη σημασία και την πυκνότητα εμφάνισης των τεκτονικών δομών
της περιοχής μελέτης.
γ) Να προσδιορίσουμε τη συμμετρία, και τις σχέσεις των τεκτονικών δομών μεταξύ
τους (ac-, bc-, ab- διακλάσεις κλπ).
δ) Να απεικονίσουμε παραστατικά σ' ένα διάγραμμα την εικόνα της τεκτονικής δομής
μιας περιοχής.
Κάθε διάγραμμα αναφέρεται για μια συγκεκριμένη περιοχή και ισχύει μόνο για εκείνη τη θέση, όπου έγιναν οι μετρήσεις. Μόνο με συγκρίσεις τέτοιων διαγραμμάτων από γειτονικές περιοχές, καταλήγουμε σε συμπεράσματα για την ευρύτερη περιοχή που αναφέρεται ένα σύνολο διαγραμμάτων.
Τα σημαντικότερα από τα διαγράμματα
αυτά είναι:
α) Τα ροδοδιαγράμματα
β) Τα διαγράμματα Schmidt
Θα πρέπει τέλος να τονισθεί, ότι η επιλογή των τεκτονικών στοιχείων που θα μετρηθούν, πρέπει να γίνεται με τέτοιον τρόπο, έτσι ώστε αυτά να είναι, κατά το δυνατόν, αντιπροσωπευτικά της τεκτονικής δομής της περιοχής.
Ιδίως θα πρέπει να αποφεύγονται περιπτώσεις υποτονισμού, λόγω διαφόρων συνθηκών, (π.χ. θέση παρατήρησης, κάλυψη της περιοχής από βλάστηση, διεύθυνση τομής κλπ), τεκτονικών δομών, που πιθανόν, να αποτελούν σημαντικά τεκτονικά στοιχεία της περιοχής μελέτης.
Έτσι δεν πρέπει να αρκείται κανείς σε μεμονωμένες παρατηρήσεις, αλλά αντίθετα, για να ερμηνευθούν με τον καλλίτερο τρόπο τα προβλήματα της τεκτονικής δομής μιας περιοχής, χρειάζεται η σύνθεση και η στατιστική επεξεργασία, όσο το δυνατόν περισσότερων παρατηρήσεων και μετρήσεων τεκτονικών στοιχείων σε διαφορετικές θέσεις.
Για κάθε θέση, βέβαια, (φυσική ή τεχνητή τομή, ρέματα κλπ) θα πρέπει να αντιστοιχεί ένα διάγραμμα.
Τα ροδοδιαγράμματα μπορούν να
διαιρεθούν σε δυο μεγάλες κατηγορίες:
α) Στα ροδοδιαγράμματα παρατάξεων
β) Στα ροδοδιαγράμματα διευθύνσεων και γωνιών κλίσεων
Συνήθως η χρησιμοποίηση των ροδοδιαγραμμάτων συνδέεται με τη μελέτη ρηξιγενών τεκτονικών δομών (διακλάσεις, κανονικά ρήγματα).
Για την κατασκευή των ροδοδιαγραμμάτων χρησιμοποιείται ως βοηθητικό υπόβαθρο, ένα δίκτυο που προκύπτει από την ορθή (πολική) προβολή μεσημβρινών και παραλλήλων κύκλων της σφαίρας πάνω στο ισημερινό επίπεδο (Σχ. Κ. 16).
 |
Σχ. Κ.16: Δίκτυο ορθής (πολικής) προβολής μεσημβρινών και παραλλήλων κύκλων της σφαίρας στο ισημερινό επίπεδο. |
Σε γενικές γραμμές για την κατασκευή ενός ροδοδιαγράμματος ακολουθούμε την εξής πορεία:
α) Λήψη μετρήσεων με τη γεωλογική πυξίδα, της παράταξης, διεύθυνσης κλίσης και γωνίας κλίσης των τεκτονικών δομών. Τις μετρήσεις τις σημειώνουμε σε μπλοκάκι και δίπλα από κάθε μέτρηση αναγράφουμε συμβολικά, την τεκτονική δομή που αναφέρεται η μέτρηση (π.χ. 350/40 ΚΙ ή 40/15 St κ.ο.), καθώς και μια πρώτη κατ' εκτίμηση ένδειξη της αξίας και του μεγέθους της τεκτονικής δομής, ή οτιδήποτε άλλο θεωρήσουμε σημαντικό (π.χ. πληρωμένες διακλάσεις με χαλαζιακό υλικό κ.ά.).
β) Σημείωση πάνω στο γεωλογικό χάρτη της θέσης, όπου έγιναν οι μετρήσεις των αντίστοιχων τεκτονικών δομών (όπως τονίσαμε ένα διάγραμμα ισχύει για εκείνη τη θέση μόνο απ' όπου πάρθηκαν οι μετρήσεις. Για το λόγο αυτό θα πρέπει επακριβώς να γνωρίζουμε το σημείο αυτό).
γ) Κατάταξη των μετρήσεων σε ομάδες που θα περιέχουν όμοια
τεκτονικά στοιχεία. Π.χ. όλες τις μετρήσεις που αναφέρονται σε διακλάσεις σε
μια ομάδα κ.ο.
δ) Κατασκευή πινάκων.
ε) Κατασκευή ροδοδιαγράμματος (Γραφική αναπαράσταση δηλαδή των διαφόρων
μετρήσεων στο πολικό δίκτυο προβολής).
Παρακάτω παραθέτουμε ένα παράδειγμα κατασκευής ενός ροδοδιαγράμματος παρατάξεων.
Έστω ότι από την εργασία μας στο ύπαιθρο, πήραμε μια σειρά μετρήσεων από παρατάξεις διακλάσεων (Σύνολο 85) που αναγράφονται στην επόμενη σελίδα.
Τις μετρήσεις αυτές θα πρέπει να τις κατατάξουμε σε ομάδες μικρών τόξων, (από 0-360° ή εφόσον πρόκειται για ροδοδιαγράμματα παρατάξεων από 0-180°), το εύρος των οποίων εξαρτάται τόσο από τη δική μας κρίση, όσο και από το αντικείμενο έρευνας. Στην περίπτωση π.χ. που μελετούμε τις σχέσεις μεταξύ κατατμήσεων δυο ή περισσοτέρων γενεών (ηλικιών), θα χρειασθεί να γίνει λεπτομερής ανάλυση αυτών και συνεπώς απαιτείται μικρός εύρος τόξων (π.χ. 5°).
Αντίθετα σε μια ευρύτερη τεκτονική μελέτη, όπου οι διακλάσεις, δεν θα αποτελούν το κύριο αντικείμενο έρευνας, το εύρος του τόξου δυνατόν να είναι μεγαλύτερο (π.χ. 10° ή και 20°).
Κατά τη στατιστική αξιοποίηση, εξ' άλλου, μετρήσεων, σε μια κοιτασματολογική μελέτη, όπου ερευνάται η σχέση της μεταλλοφορίας και των ρηξιγενών επιφανειών, ή σε αντικείμενα έρευνας της Τεχνικής Γεωλογίας (π.χ. συσχέτιση της επούλωσης ρηγμάτων με τη διεύθυνση τους, κατασκευή ενός τούνελ κ.ά.) εκλέγονται τόξα μικρού εύρους.
Για την κατάταξη λοιπόν των μετρήσεων σε ομάδες μικρών τόξων (π.χ. 10°) και στη συνέχεια, την κατασκευή του αντίστοιχου ροδοδιαγράμματος χρησιμοποιούμε τον πίνακα Ι.
- Η πρώτη σειρά περιλαμβάνει τη μέση τιμή των μικρών αυτών
τόξων από 0° έως 170°.
- Η δεύτερη σειρά περιλαμβάνει με ακρίβεια τις ακραίες τιμές του κάθε τόξου.
Π.χ. το τόξο που έχει μέση τιμή 10° περιέχεται μεταξύ των τιμών 6° μέχρι 15°
κ.ο.κ.
- Η τρίτη σειρά αποτελεί τη συνέχεια της πρώτης και περιέχει τιμές από 180° έως
350°. Οι τιμές αυτές για κάθε τόξο διαφέρουν 180° από τις αντίστοιχες τιμές της
πρώτης σειράς, έτσι ώστε στον κύκλο αποτελούν τα συμμετρικά αντίθετα σημεία
αυτών.
- Η τέταρτη σειρά αποτελεί, επίσης, τη συνέχεια της
δεύτερης σειράς, με συμμετρικές αντίθετες τιμές (διαφέρουν 180°), από αυτές της
δεύτερης σειράς.
- Στην πέμπτη σειρά αναγράφουμε με απλό γραμμικό τρόπο, το πλήθος των μετρήσεων
που αντιστοιχούν στο εύρος κάθε τόξου, που περιλαμβάνονται στη δεύτερη και
τέταρτη σειρά.
Στην προκειμένη περίπτωση των ροδοδιαγραμμάτων παρατάξεων, μετρήσεις με τιμές
που διαφέρουν κατά 180°, όπως είναι φυσικό, θα σημειώνονται μαζί. Π.χ. δυο
μετρήσεις με τιμές 5° και 185° αντίστοιχα θα ανήκουν στην ίδια ομάδα.
|
85 μετρήσεις παρατάξεων διακλάσεων |
|||||
|
30 |
42 |
230 |
92 |
308 |
135 |
|
35 |
216 |
50 |
130 |
310 |
138 |
|
28 |
215 |
55 |
135 |
130 |
139 |
|
30 |
220 |
90 |
125 |
135 |
137 |
|
207 |
222 |
95 |
126 |
308 |
316 |
|
208 |
224 |
92 |
128 |
315 |
320 |
|
215 |
215 |
88 |
128 |
305 |
316 |
|
40 |
39 |
86 |
135 |
306 |
325 |
|
37 |
40 |
88 |
132 |
130 |
318 |
|
40 |
45 |
90 |
306 |
135 |
326 |
|
45 |
222 |
266 |
315 |
125 |
335 |
|
38 |
238 |
270 |
307 |
140 |
330 |
|
39 |
226 |
275 |
310 |
136 |
150 |
|
42 |
228 |
270 |
315 |
145 |
146 |
|
|
|
|
|
|
155 |
Πίνακας Ι
|
1 |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
140 |
150 |
160 |
170 |
|
2 |
356 |
6 |
16 |
26 |
36 |
46 |
56 |
66 |
76 |
86 |
96 |
106 |
116 |
126 |
136 |
146 |
156 |
166 |
|
5 |
15 |
25 |
35 |
45 |
55 |
65 |
75 |
85 |
95 |
105 |
115 |
125 |
135 |
145 |
155 |
165 |
175 |
|
|
3 |
180 |
190 |
200 |
210 |
220 |
230 |
240 |
250 |
260 |
270 |
280 |
290 |
300 |
310 |
320 |
330 |
340 |
350 |
|
4 |
176 |
186 |
196 |
206 |
216 |
226 |
236 |
246 |
256 |
266 |
276 |
286 |
296 |
306 |
316 |
326 |
336 |
346 |
|
185 |
195 |
205 |
215 |
225 |
235 |
245 |
255 |
265 |
275 |
285 |
295 |
305 |
315 |
325 |
335 |
345 |
355 |
|
| 5 | V | V | V | I | V | V | V | VI | ||||||||||
| II | V | V | V | V | ||||||||||||||
| V | II | V | II | |||||||||||||||
| III | V | |||||||||||||||||
| IV | ||||||||||||||||||
| 6 | 7 | 18 | 5 | 1 | 12 | 24 | 12 | 6 | ||||||||||
| 7 | 17.5 | 45 | 12.5 | 2.5 | 30 | 60 | 30 | 15 |
- Στην έκτη σειρά γράφουμε με αριθμό το πλήθος των
μετρήσεων που περιέχονται σε κάθε τετράγωνο της πέμπτης σειράς.
- Η έβδομη σειρά περιλαμβάνει αριθμούς που δείχνουν αναλογικά τι μήκος θα
αντιπροσωπεύει κάθε αριθμός της έκτης σειράς, αν ο μεγαλύτερος από αυτούς ή το
σύνολο των μετρήσεων, έχει μήκος 60 mm (Όσο δηλαδή είναι το μήκος της ακτίνας
του κύκλου, που θα χρησιμοποιηθεί για την κατασκευή του ροδοδιαγράμματος).
Αν π.χ. ο αριθμός 24 (ο μεγαλύτερος της σειράς) ή ο αριθμός 85 (το σύνολο των μετρήσεων) αντιπροσωπεύει ένα μήκος 60 mm, τότε οι άλλοι αριθμοί θα πάρουν τα ανάλογα μήκη. Στο παρόν παράδειγμα οι 24 μετρήσεις αντιστοιχούν σε 60 mm κ.ο.κ.
Μετά τη μετατροπή των μετρήσεων σε μήκη, με βάση, α) το δίκτυο της πολικής προβολής, β) τους αριθμούς που θα προκύψουν (δεδομένα δηλαδή της εβδόμης σειράς) και γ) τα δεδομένα της πρώτης και τρίτης σειράς, κατασκευάζουμε στην ουσία μια γραφική παράσταση των στοιχείων της εβδόμης σειράς που είναι το ροδοδιάγραμμα.
Έτσι σε κάθε ευθεία που συνδέει τα μέσα των τόξων, που διαιρέσαμε τον κύκλο, με το κέντρο του δικτύου της πολικής προβολής, σημειώνουμε ένα σημείο σε τόση απόσταση από το κέντρο, όση είναι το μήκος που προέκυψε από τη μετατροπή του αντίστοιχου αριθμού μετρήσεων (τιμές έβδομης σειράς), που περιέχονταν σε κάθε τόξο.
Τα διαδοχικά σημεία που θα προκύψουν τα ενώνουμε με μια γραμμή, ενώ τα υπόλοιπα τα συνδέουμε απευθείας με μια γραμμή με το κέντρο του κύκλου.
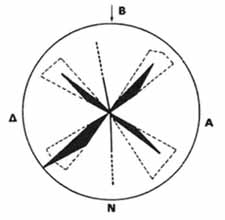
Το σχήμα που κατασκευάστηκε τελικά, μ' αυτόν τον τρόπο, αποτελεί και το επιθυμητό ροδοδιάγραμμα (Σχ. Κ. 17).
Το ροδοδιάγραμμα αυτό προφανώς αποτελείται από δυο όμοια σκέλη συμμετρικά ως προς το κέντρο του κύκλου, έτσι ώστε, να είναι δυνατόν το ζητούμενο αποτέλεσμα να δίνεται με την αναγραφή μόνο του ενός σκέλους.
Αυτό δε συμβαίνει, φυσικά, με τα ροδοδιαγράμματα διευθύνσεων κλίσεων κα γωνιών κλίσεων, όπου κάθε σκέλος απεικονίζει και μια διαφορετική ομάδα μετρήσεων.
 |
Σχ. Κ. 17: Ροδοδιάγραμμα παρατάξεων |
Η διαφορά των ροδοδιαγραμμάτων αυτών, από τα αντίστοιχα των παρατάξεων, είναι ότι αυτά αναφέρονται στις διευθύνσεις και γωνίες κλίσεων των γεωλογικών σχηματισμών, με αποτέλεσμα να δίνουν με μεγαλύτερη λεπτομέρεια την εικόνα της ρηξιγενούς τεκτονικής δομής μιας περιοχής.
Παρακάτω παραθέτουμε ένα παράδειγμα κατασκευής ενός τέτοιου ροδοδιαγράμματος.
Έστω ότι μετρήσαμε στο ύπαιθρο 150 επιφάνειες διακλάσεων. Τα στοιχεία των επιφανειών αυτών αναγράφονται στις επόμενες σελίδες και με τους δυο γνωστούς τρόπους. Κατά τον πρώτο αναγράφεται η παράταξη, η γωνία κλίσεως και η διεύθυνση κλίσης της επιφάνειας, ενώ κατά τον δεύτερο (οι αριθμοί σε παρένθεση) αναγράφεται μόνο η διεύθυνση κλίσης και η γωνία κλίσης.
| 85 μετρήσεις παρατάξεων και γωνιών κλίσεως διακλάσεων | ||
|
30/80 ΝΑ (120/80) |
230/78 ΝΑ (140/78) |
136/85 ΝΔ (226/85) |
|
35/85 ΝΑ (125/85) |
50/85 ΝΑ (140/85) |
145/78 ΝΔ (235/78) |
|
28/78 ΝΑ (118/78) |
55/82 ΝΑ (145/82) |
135/80 ΝΔ (225/80) |
|
30/75 ΝΑ (120/75) |
90/80 Ν (180/80) |
138/85 ΝΔ (228/85) |
|
207/82 ΝΑ (117/82) |
95/82 Ν (185/82) |
139/78 ΝΔ (229/78) |
|
208/80 ΝΑ (118/80) |
92/80 Ν (182/80) |
137/75 ΝΔ (227/75) |
|
215/90 ΝΑ (125/90) |
88/85 Ν (178/85) |
316/82 ΝΔ (226/82) |
|
40/85 ΝΑ (130/85) |
86/72 Ν (176/72) |
320/80 ΝΔ (230/80) |
|
37/80 ΝΑ (127/80) |
88/75 Ν (178/75) |
316/85 ΝΔ (226/85) |
|
40/82 ΝΑ (130/82) |
90/85 Ν (180/85) |
325/72 ΝΔ (235/72) |
|
45/75 ΝΑ (135/75) |
266/90 Ν (176/90) |
318/70 ΝΔ (228/70) |
|
38/72 ΝΑ (128/72) |
270/88 Ν (180/88) |
140/82 ΝΔ (230/82) |
|
39/78 ΝΑ (129/78) |
275/78 Ν (185/78) |
142/78 ΝΔ (232/78) |
|
42/80 ΝΑ (132/80) |
270/75 Ν (180/75) |
136/80 ΝΔ (226/80) |
|
42/88 ΝΑ (132/88) |
92/78 Ν (182/78) |
145/78 ΝΔ (235/78) |
|
216/80 ΝΑ (126/80) |
130/80 ΝΔ (220/80) |
137/82 ΝΔ (227/82) |
|
215/85 ΝΑ (125/85) |
135/85 ΝΔ (225/85) |
139/80 ΝΔ (229/80) |
|
220/82 ΝΑ (130/82) |
125/80 ΝΔ (215/80) |
140/82 ΝΔ (230/82) |
|
222/86 ΝΑ (132/86) |
126/82 ΝΔ (216/82) |
141/90 ΝΔ (231/90) |
|
224/85 ΝΑ (134/85) |
128/78 ΝΔ (218/78) |
142/90 ΝΔ (232/90) |
|
215/80 ΝΑ (125/80) |
128/74 ΝΔ (218/74) |
140/88 ΝΔ (230/88) |
|
39/70 ΝΑ (129/70) |
135/78 ΝΔ (225/78) |
144/85 ΝΔ (234/85) |
|
40/72 ΝΑ (130/72) |
132/85 ΝΔ (222/85) |
145/82 ΝΔ (235/82) |
|
45/75 ΝΑ (135/75) |
306/80 ΝΔ (216/80) |
326/85 ΝΔ (236/85) |
|
222/82 ΝΑ (132/82) |
315/78 ΝΔ (225/78) |
335/80 ΝΔ (245/80) |
|
238/85 ΝΑ (148/85) |
307/80 ΝΔ (217/80) |
330/78 ΝΔ (240/78) |
|
226/85 ΝΑ (136/85) |
310/75 ΝΔ (220/75) |
150/75 ΝΔ (240/75) |
|
228/72 ΝΑ (138/72) |
140/80 ΝΔ (230/80) |
146/78 ΝΔ (236/78) |
Σε γενικές γραμμές η πορεία που ακολουθούμε για την κατασκευή των ροδοδιαγραμμάτων αυτών είναι παρόμοια με αυτή των ροδοδιαγραμμάτων παρατάξεων, με ορισμένες μικροδιαφορές, που τις επισημαίνουμε παρακάτω.
Έτσι, στην αρχή κατασκευάζουμε δυο πίνακες (πίνακας II και ΙΙ΄). Στους πίνακες αυτούς οι επτά πρώτες σειρές περιέχουν στοιχεία όμοια με αυτά του πίνακα Ι, που χρησιμοποιήσαμε για την κατασκευή του ροδοδιαγράμματος παρατάξεων.
Η διαφορά αυτών των δυο πινάκων είναι, ότι ο ένας περιέχει διευθύνσεις κλίσεων Δ, ΒΔ, Β, ΒΑ και ΑΒΑ, ενώ ο άλλος Α, ΝΑ, Ν, ΝΔ και ΔΝΔ. Στον πρώτο, (πίνακας II), αναγράφονται δηλαδή οι μετρήσεις που αναφέρονται στο βόρειο ημισφαίριο και στον δεύτερο, (πίνακας ΙI΄), αυτές που αναφέρονται στο νότιο ημισφαίριο.
| 65 μετρήσεις παρατάξεων και γωνιών κλίσεως διακλάσεων | ||
|
30/85 ΒΔ (300/85) |
220/80 ΒΔ (310/80) |
128/78 ΒΑ (38/78) |
|
26/80 ΒΔ (296/80) |
224/85 ΒΔ (314/85) |
131/83 ΒΑ (41/83) |
|
35/88 ΒΔ (305/88) |
50/75 ΒΔ (320/75) |
132/85 ΒΑ (42/85) |
|
210/80 ΒΔ (300/80) |
235/78 ΒΔ (325/78) |
130/90 ΒΑ (40/90) |
|
206/85 ΒΔ (296/85) |
80/78 Β (350/78) |
130/88 ΒΑ (40/88) |
|
212/75 ΒΔ (302/75) |
76/85 Β (346/85) |
133/90 ΒΑ (43/90) |
|
40/88 ΒΔ (310/88) |
78/80 Β (348/80) |
135/80 ΒΑ (45/80) |
|
36/80 ΒΔ (306/80) |
85/75 Β (355/75) |
135/88 ΒΑ (45/88) |
|
45/75 ΒΔ (315/75) |
260/72 Β (350/72) |
134/78 ΒΑ (44/78) |
|
38/82 ΒΔ (308/82) |
256/75 Β (346/75) |
310/80 ΒΑ (40/80) |
|
40/84 ΒΔ (310/84) |
256/82 Β (346/82) |
310/85 ΒΑ (40/85) |
|
37/85 ΒΔ (307/85) |
258/78 Β (348/78) |
306/88 ΒΑ (36/88) |
|
39/86 ΒΔ (309/86) |
260/75 Β (350/75) |
315/85 ΒΑ (45/84) |
|
40/75 ΒΔ (310/75) |
262/78 Β (352/78) |
140/80 ΒΑ (50/80) |
|
42/78 ΒΔ (312/78) |
120/80 ΒΑ ( 30/80) |
141/85 ΒΑ (51/85) |
|
43/79 ΒΔ (313/79) |
125/75 ΒΑ ( 35/75) |
136/80 ΒΑ (46/80) |
|
44/82 ΒΔ (314/82) |
300/82 ΒΑ ( 30/82) |
145/90 ΒΑ (55/90) |
|
45/85 ΒΔ (315/85) |
130/80 ΒΑ ( 40/80) |
138/78 ΒΑ (48/78) |
|
220/78 ΒΔ (310/78) |
126/75 ΒΑ ( 36/75) |
142/75 ΒΑ (52/75) |
|
216/72 ΒΔ (306/72) |
135/82 ΒΑ ( 45/82) |
140/78 ΒΑ (50/78) |
|
225/74 ΒΔ (315/74) |
127/78 ΒΑ ( 37/78) |
320/82 ΒΑ (50/82) |
|
218/78 ΒΔ (308/78) |
129/75 ΒΑ ( 39/75) |
|
Πίνακας ΙI
| Δ | ΒΔ | Β | ΒΑ | Α | ||||||||||||||
|
1 |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
140 |
150 |
160 |
170 |
|
2 |
356 |
6 |
16 |
26 |
36 |
46 |
56 |
66 |
76 |
86 |
96 |
106 |
116 |
126 |
136 |
146 |
156 |
166 |
|
5 |
15 |
25 |
35 |
45 |
55 |
65 |
75 |
85 |
95 |
105 |
115 |
125 |
135 |
145 |
155 |
165 |
175 |
|
|
3 |
180 |
190 |
200 |
210 |
220 |
230 |
240 |
250 |
260 |
270 |
280 |
290 |
300 |
310 |
320 |
330 |
340 |
350 |
|
4 |
176 |
186 |
196 |
206 |
216 |
226 |
236 |
246 |
256 |
266 |
276 |
286 |
296 |
306 |
316 |
326 |
336 |
346 |
|
185 |
195 |
205 |
215 |
225 |
235 |
245 |
255 |
265 |
275 |
285 |
295 |
305 |
315 |
325 |
335 |
345 |
355 |
|
| 5 | V | V | II | I | V | III | V | V | ||||||||||
| I | V | V | V | III | ||||||||||||||
| V | V | |||||||||||||||||
| III | III | |||||||||||||||||
| 6 | 6 | 18 | 2 | 1 | 10 | 3 | 18 | 12 | ||||||||||
| 7 | 15 | 45 | 5 | 2.5 | 25 | 7.5 | 45 | 30 | ||||||||||
| 85 | 88 | 75 | 78 | 80 | 80 | 80 | ||||||||||||
| 8 | 80 | 80 | 78 | 85 | 75 | 75 | 85 | |||||||||||
| 88 | 75 | 80 | 82 | 82 | 80 | |||||||||||||
| 9 | 82 | 80 | 76 | 78 | 79 | 83 | 81 | |||||||||||
| 10 | 270 | 280 | 290 | 300 | 310 | 320 | 330 | 340 | 350 | 360 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| 11 | 55 | 53 | 51 | 52 | 53 | 55 | 54 |
Πίνακας ΙI
| Δ | ΒΔ | Β | ΒΑ | Α | ||||||||||||||
|
1 |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
140 |
150 |
160 |
170 |
|
2 |
356 |
6 |
16 |
26 |
36 |
46 |
56 |
66 |
76 |
86 |
96 |
106 |
116 |
126 |
136 |
146 |
156 |
166 |
|
5 |
15 |
25 |
35 |
45 |
55 |
65 |
75 |
85 |
95 |
105 |
115 |
125 |
135 |
145 |
155 |
165 |
175 |
|
|
3 |
180 |
190 |
200 |
210 |
220 |
230 |
240 |
250 |
260 |
270 |
280 |
290 |
300 |
310 |
320 |
330 |
340 |
350 |
|
4 |
176 |
186 |
196 |
206 |
216 |
226 |
236 |
246 |
256 |
266 |
276 |
286 |
296 |
306 |
316 |
326 |
336 |
346 |
|
185 |
195 |
205 |
215 |
225 |
235 |
245 |
255 |
265 |
275 |
285 |
295 |
305 |
315 |
325 |
335 |
345 |
355 |
|
| 5 | V | V | V | I | V | V | V | V | ||||||||||
| II | V | V | V | V | I | |||||||||||||
| V | II | II | V | |||||||||||||||
| III | V | |||||||||||||||||
| III | ||||||||||||||||||
| 6 | 7 | 18 | 5 | 1 | 12 | 12 | 24 | 6 | ||||||||||
| 7 | 17.5 | 45 | 12.5 | 2.5 | 30 | 30 | 60 | 15 | ||||||||||
| 85 | 85 | 85 | 85 | 80 | 80 | 80 | 85 | |||||||||||
| 8 | 85 | 80 | 72 | 82 | 85 | 85 | 80 | |||||||||||
| 78 | 82 | 78 | 80 | 80 | 78 | 78 | ||||||||||||
| 9 | 81 | 80 | 80 | 85 | 81 | 80 | 81 | 81 | ||||||||||
| 10 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | 210 | 220 | 230 | 240 | 250 | 260 |
| 11 | 54 | 53 | 53 | 57 | 54 | 53 | 54 | 54 |
Έτσι δυο τιμές με την ίδια παράταξη αλλά με αντίθετες διευθύνσεις κλίσεων θα αναγράφονται στο ίδιο τόξο, αλλά σε διαφορετικό πίνακα, ανάλογα με τη διεύθυνση κλίσης. Γενικά, για την καταγραφή μιας μέτρησης σε κάποιο τόξο του πίνακα θα λαμβάνεται υπόψη και η διεύθυνση κλίσης της επιφάνειας. Π.χ. η διάκλαση με τιμές 60/30 ΒΔ θα καταγραφεί στον πίνακα ΙΙ, αφού η διεύθυνση κλίσης είναι ΒΔ. Αντίθετα η διάκλαση με τιμές 60/30 ΝΑ θα περαστεί στον πίνακα II', στο αντίστοιχο τόξο φυσικά.
- Η όγδοη
σειρά, περιέχει τις γωνίες κλίσεων των μετρήσεων της 5ης και 6ης σειράς.
- Η ένατη σειρά περιέχει τον μέσο
όρο των τιμών των γωνιών της όγδοης σειράς.
|
(ΜΟ
= |
- Η δεκάτη
σειρά περιέχει τη μέση τιμή του τόξου που κατευθύνεται η διεύθυνση κλίσης και
φυσικά διαφέρει 90° από την αντίστοιχη τιμή του τόξου της πρώτης και τρίτης
σειράς, που αναφέρονται οι παρατάξεις.
- Η εντεκάτη σειρά περιέχει
αριθμούς που δείχνουν αναλογικά τι μήκος θα αντιπροσωπεύει κάθε αριθμός της 9ης
σειράς, λαμβάνοντας υπόψη, ότι γωνία κλίσεως 90° συμβολίζεται μ' ένα
μήκος, όσο είναι η ακτίνα του κύκλου (60 mm), που θα χρησιμοποιηθεί για το
ροδοδιάγραμμα. Έτσι π.χ. μια γωνία κλίσεως 81°, θα αναλογεί σ' ένα μήκος 54 mm
κ.ο.κ.
Η πορεία για την κατασκευή του σχήματος του ροδοδιαγράμματος διευθύνσεων κλίσεων είναι παρόμοια με αυτή του ροδοδιαγράμματος παρατάξεων (Σχ. Κ.18). Η διαφορά περιορίζεται στο γεγονός ότι, για το ροδοδιάγραμμα διευθύνσεων κλίσεων, χρησιμοποιούμε τα στοιχεία της 10ης και της 7ης σειράς, με τον ίδιο φυσικά τρόπο.
Επίσης, για να συμβολίσουμε στο ίδιο διάγραμμα τις σχέσεις των γωνιών κλίσεων των επιφανειών που μετρήθηκαν, ενώνουμε με διακεκομμένη γραμμή, για διάκριση, τα σημεία που προκύπτουν από τα δεδομένα των σειρών 10 και 11 (Σχ. Κ.18).
Μ' αυτόν τον τρόπο στο ίδιο ροδοδιάγραμμα απεικονίζονται όλα τα στοιχεία μιας επιφάνειας (παράταξη, διεύθυνση κλίσης και γωνία κλίσης), έτσι ώστε να έχουμε λεπτομερέστερη απεικόνιση της τεκτονικής δομής που μελετάμε.
Φυσικά, εκτός από τις δυο μεγάλες αυτές κατηγορίες ροδοδιαγραμμάτων που περιγράψαμε, υπάρχει ακόμη μια σειρά και άλλων τρόπων παραστατικής απεικόνισης των τεκτονικών δεδομένων μιας περιοχής (Σχ. Κ. 19).
Οι μέθοδοι αυτοί όμως δεν παρουσιάζουν κάποιο ιδιαίτερο ενδιαφέρον, γι' αυτό και περιοριστήκαμε στην ανάπτυξη μόνο των παραπάνω δυο τρόπων στατιστικής επεξεργασίας των μετρήσεων.
 |
|
| Σχ. Κ. 18: Ροδοδιάγραμμα διευθύνσεων και γωνιών κλίσεων. | |
 |
Σχ. Κ.19: Διαγράμματα παραστατικής απεικόνισης διαφόρων τεκτονικών δεδομένων (C.T.H. 2, 1965). |
Κ. 2.2. Διαγράμματα Schmidt - δίκτυο Schmidt
Τις μεθόδους της παραστατικής απεικόνισης και στατιστικής επεξεργασίας τεκτονικών στοιχείων στο δίκτυο Schmidt (διαγράμματα Schmidt), ανέπτυξαν κατά κύριο λόγο οι Schmidt (1932) και Sander (1948-50).
Σε αντίθεση με τα ροδοδιαγράμματα (μελέτη μόνο των ρηξιγενών δομών) τα διαγράμματα Schmidt, είναι δυνατόν να εφαρμοσθούν για τη μελέτη όλου του φάσματος των τεκτονικών δομών, ρηξιγενών και πτυχογόνων. Για το λόγο αυτό και από το γεγονός, ότι η τεκτονική δομή μιας περιοχής είναι δυνατόν να απεικονισθεί και να μελετηθεί λεπτομερέστερα με τα διαγράμματα αυτά, τον τελευταίο καιρό επικράτησε να χρησιμοποιούνται, κυρίως αυτά, κατά την τεκτονική μελέτη μιας περιοχής, παρά τα ροδοδιαγράμματα. Τα τελευταία εφαρμόζονται όλο και πιο σπάνια και σε ειδικές μόνο περιπτώσεις.
Τα διαγράμματα Schmidt δεν είναι τίποτε άλλο, παρά η προβολή και απεικόνιση στο δίκτυο Schmidt των τεκτονικών στοιχείων, με κάποια ορισμένη μεθοδολογία (βλ. παρακάτω).
Το δίκτυο Schmidt προκύπτει από τη στερεογραφική (αζιμουθιακή) προβολή των μεσημβρινών και παραλλήλων κύκλων μιας σφαίρας, σ' ένα επίπεδο κάθετο στο ισημερινό επίπεδο, ώστε επιφάνειες της προβαλλόμενης σφαίρας (τετραγωνίδια που σχηματίζονται από την τομή των μεσημβρινών και παραλλήλων κύκλων), προβάλλονται σε ισοεμβαδικές επιφάνειες, διαφορετικού όμως σχήματος (Σχ. Κ.21β).
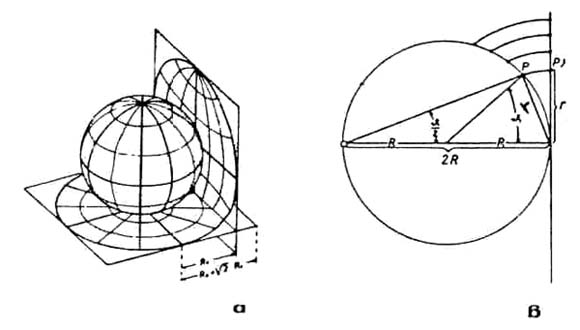 |
| Σχ. Κ.20: α) Προβολή σφαίρας σε ένα επίπεδο κάθετο στον ισημερινό, καθώς και στον ισημερινό, β) Γεωμετρικές συνθήκες της προβολής, για την κατασκευή του δικτύου Schmidt (Murawski, 1977, Metz, 1967). |
Αυτό επιτυγχάνεται εφόσον κατά την αζιμουθιακή προβολή οι χορδές της σφαίρας διατηρήσουν το μήκος τους. Με το σκεπτικό αυτό κάθε σημείο Ρ της σφαίρας, ακτίνας R και γωνιακής απόστασης θ, προβάλλεται στο δίκτυο, διατηρώντας το μήκος της χορδής του r, που δίδεται από τον τύπο r = 2Rημθ/2 (Σχ. Κ.20β). Δια θ = 90° μπορούμε να υπολογίσουμε την ακτίνα του δικτύου, που θα είναι: r = 2Rημ45°.
Στο δίκτυο Wulf, που αποτελεί ένα ανάλογο με το δίκτυο Schmidt δίκτυο, η απόσταση r δίδεται από τον τύπο r = 2Rεφθ/2.
Επί πλέον, η διαφορά τους βρίσκεται στο γεγονός, ότι με τη βοήθεια του δικτύου WuIf επιτυγχάνεται η πιστή αναπαράσταση γωνιών (χρησιμοποιείται κυρίως από την Ορυκτολογία), ενώ με το δίκτυο Schmidt, η πιστή αναπαράσταση επιφανειών (Σχ. Κ.21).
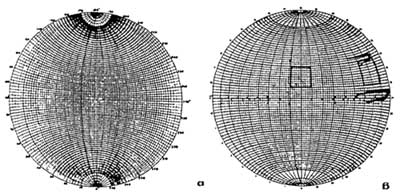 |
| Σχ. Κ.21: α) Δίκτυο Wulf. β) Δίκτυο Schmidt. |
Στα επόμενα θα αναπτύξουμε με ποιον τρόπο κατασκευάζεται ένα διάγραμμα με τη βοήθεια του δικτύου Schmidt.
Ακόμη θα δειχθεί πώς εμφανίζονται ορισμένες τεκτονικές δομές πάνω στο διάγραμμα, πώς απεικονίζονται οι μεταξύ τους σχέσεις και τέλος σε τι συμπεράσματα είναι δυνατόν να οδηγηθούμε, από την εικόνα της τεκτονικής υφής, που θα προκύψει πάνω στο διάγραμμα.
Κ. 2.2.1. Παράσταση των τεκτονικών δομών με τη βοήθεια του δικτύου Schmidt
Το μεγαλύτερο μέρος των τεκτονικών δομών, όπως τονίσθηκε, εμφανίζεται είτε ως ένα επιφανειακό, είτε ως ένα γραμμικό στοιχείο.
θα εξετάσουμε έτσι τις δυνατότητες αναπαράστασης μιας επιφάνειας και μιας γράμμωσης στο δίκτυο Schmidt.
Μια επιφάνεια απεικονίζεται στο δίκτυο Schmidt είτε ως μέγιστος κύκλος είτε ως πόλος.
Η αναπαράσταση μιας επιφάνειας προκύπτει ως εξής: Αν δεχθούμε ότι ένα επίπεδο διέρχεται από το κέντρο της σφαίρας, τότε η γραμμή της τομής του επιπέδου με το κάτω ημισφαίριο (στην τεκτονική ανάλυση προβάλλουμε κατά συνθήκη στο δίκτυο Schmidt, τις τομές των επιφανειακών ή γραμμικών στοιχείων με το κάτω ημισφαίριο), θα προβάλλεται στο οριζόντιο επίπεδο, που συμπίπτει στην προκειμένη περίπτωση με το δίκτυο Schmidt, ως μέγιστος κύκλος του δικτύου (Σχ. Κ.22).
Κατακόρυφες, συνεπώς, επιφάνειες θα απεικονίζονται στο δίκτυο Schmidt, ως ευθείες γραμμές, οριζόντιες επιφάνειες θα συμπίπτουν με την περιφέρεια του δικτύου, ενώ κεκλιμμένες επιφάνειες θα εμφανίζονται ως κεκαμμένες γραμμές, με τόσο μεγαλύτερη κυρτότητα, όσο μικρότερη κλίση έχει η επιφάνεια.
Η ευθεία που διέρχεται από το κέντρο της σφαίρας και είναι κάθετη σε μια δεδομένη επιφάνεια, τέμνει το κάτω ημισφαίριο σε κάποιο σημείο.
Η προβολή του σημείου αυτού στο οριζόντιο επίπεδο αντιστοιχεί στον πόλο της συγκεκομμένης επιφάνειας.
Ο πόλος συνεπώς μιας τεκτονικής επιφάνειας βρίσκεται πάντοτε σε γωνιακή απόσταση 90° από τον μέγιστο κύκλο της αντίστοιχης επιφάνειας (Σχ. Κ.22).
Όσο μεγαλύτερη κλίση έχει, λοιπόν, η επιφάνεια τόσο ο πόλος της θα πλησιάζει προς την περιφέρεια του δικτύου, ενώ αντίθετα, ο μέγιστος κύκλος της θα απομακρύνεται από αυτή (Σχ. Κ.22).
Ένα γραμμικό στοιχείο που διέρχεται από το κέντρο της σφαίρας θα τέμνει το κάτω ημισφαίριο σε κάποιο σημείο. Η προβολή του σημείου αυτού στο δίκτυο Schmidt καθορίζει τη θέση του πόλου του γραμμικού στοιχείου (Σχ. Κ.22).
Όσο μικρότερη, συνεπώς, γωνία κλίσεως έχει το γραμμικό στοιχείο, ο πόλος του θα πλησιάζει προς την περιφέρεια του δικτύου. Ο πόλος οριζόντιου γραμμικού στοιχείου προβάλλεται στην περιφέρεια του δικτύου, ενώ ο πόλος κατακόρυφου γραμμικού στοιχείου στο κέντρο του δικτύου.
Με τα παραπάνω γίνεται φανερό, για ποιο λόγο και με ποιο τρόπο, ένα επιφανειακό ή γραμμικό στοιχείο εμφανίζεται στα διαγράμματα Schmidt ως μέγιστος κύκλος ή πόλος και πόλος αντίστοιχα.
Κ. 2.2.2. Παράδειγμα στερεογραφικής προβολής στο δίκτυο Schmidt επιφάνειας με στοιχεία 150/60 ΒΑ
(Για όλα τα παραδείγματα που θα ακολουθήσουν ισχύει, η προβολή στο δίκτυο Schmidt των σημείων τομής των τεκτονικών δομών με το κάτω ημισφαίριο της σφαίρας).
Πάνω στο δίκτυο Schmidt, τοποθετούμε διαφανές χαρτί, στο οποίο σχεδιάζουμε την περιφέρεια του δικτύου και σημειώνουμε κανονικά τα σημεία του ορίζοντα (Σχ. Κ.23).
Για την αναπαράσταση της επιφάνειας στρέφουμε γύρω από το κέντρο του δικτύου αριστερόστροφα κατά 150° το διαφανές χαρτί (όση δηλαδή είναι η παράταξη της) (Σχ. Κ.23).
Στη συνέχεια, μετρώντας πάνω στον οριζόντιο Α-Δ άξονα του δικτύου 60° (όση είναι δηλαδή η γωνία κλίσης της επιφάνειας) από το σημείο Δ της περιφέρειας προς το κέντρο του κύκλου, χαράσσουμε στο διαφανές χαρτί τον αντίστοιχο μέγιστο κύκλο του δικτύου, που είναι και ο μέγιστος κύκλος της επιφάνειας (Σχ. Κ.23).
Για να βρούμε τον πόλο της επιφάνειας, σημειώνουμε στον Α-Δ άξονα επίσης του δικτύου και σε απόσταση 90° από το προηγούμενο σημείο, με βάση το οποίο χαράξαμε τον μέγιστο κύκλο, ένα νέο σημείο που αποτελεί και τον πόλο της επιφάνειας (Σχ. Κ.23).
Τέλος επαναφέρουμε το διαφανές χαρτί στην πρωταρχική του θέση και έχουμε έτσι τη στερεογραφική προβολή της επιφάνειας με στοιχεία 150/60 ΒΑ.
Η παραπάνω διαδικασία εφαρμόζεται σε κάθε περίπτωση για τη στερεογραφική προβολή στο δίκτυο Schmidt επιφανειακών στοιχείων. Εκείνο, το οποίο διαφέρει ανάλογα και εξαρτάται από τη διεύθυνση κλίσης της επιφάνειας είναι το σημείο (άλλοτε από την ανατολή και άλλοτε από τη δύση), από το οποίο θα αρχίσουμε να μετράμε τη γωνία κλίσης, για να φέρουμε τον μέγιστο κύκλο ή τον πόλο.
 |
Σχ. Κ.23: Παράδειγμα στερεογραφικής προβολής επιφανειακού στοιχείου στο δίκτυο Schmidt (C.T.H. 4. 1969). |
Κ. 2.2.3. Παράδειγμα στερεογραφικής προβολής γράμμωσης με στοιχεία 60/25 ΝΑ
Το γραμμικό στοιχείο όπως τονίσαμε, αναπαρίσταται στο δίκτυο Schmidt μόνο ως πόλος.
Για την προβολή του συγκεκριμένου γραμμικού στοιχείου (η διαδικασία προφανώς επεκτείνεται για κάθε γραμμικό στοιχείο), στρέφουμε το διαφανές χαρτί αριστερόστροφα, γύρω από το κέντρο του δικτύου κατά 60° (όση δηλαδή είναι η παράταξη του) (Σχ. Κ.24).
Στη συνέχεια και στον Β-Ν άξονα του δικτύου, αρχίζοντας από τον νότο προς το κέντρο, μετράμε 25° (όση δηλαδή είναι η γωνία κλίσης του γραμμικού στοιχείου) και σημειώνουμε ένα σημείο που αντιστοιχεί στον πόλο του γραμμικού στοιχείου. Τέλος επαναφέρουμε το διαφανές χαρτί στην πρωταρχική του θέση (Σχ. Κ.24).
Εκείνο που πρέπει επίσης να προσέχουμε κάθε φορά, κατά την προβολή γραμμικών στοιχείων είναι από που θα αρχίσουμε να μετράμε τη γωνία κλίσης, για να φέρουμε τον πόλο. Αυτό εξαρτάται από τη διεύθυνση βύθισης του γραμμικού στοιχείου.
Έτσι αρχίζουμε τη μέτρηση από το νότο προς το κέντρο, όταν η διεύθυνση κλίσης του γραμμικού στοιχείου είναι Δ, ΝΔ, Ν και ΝΑ, ενώ από το βορρά προς το κέντρο, όταν η διεύθυνση κλίσης είναι Α, ΒΑ, Β και ΒΔ.
 |
Σχ. Κ.24: Παράδειγμα στερεογραφικής προβολής γραμμικού στοιχείου στο δίκτυο Schmidt (C.T.H. 4, 1969). |
Κ. 2.2.4. Πυκνότητα πόλων και μέγιστη τιμή
Κατά την αναπαράσταση μεγάλου αριθμού ομοίων τεκτονικών στοιχείων στα διαγράμματα Schmidt, αποτελεί μεγάλης σημασίας γεγονός, η εξακρίβωση των μέγιστων συγκέντρωσης των τεκτονικών αυτών στοιχείων. Με τον τρόπο αυτόν επιτυγχάνεται μια πρώτη εικόνα της κύριας ανάπτυξης των τεκτονικών δομών που μελετώνται.
Όταν τα τεκτονικά αυτά στοιχεία προβάλλονται με τη μορφή πόλων, ακολουθούμε την εξής πορεία για την εξακρίβωση, με ακρίβεια, των μέγιστων συγκεντρώσεων τους (Σχ. Κ. 25).
- Κάτω από το διαφανές χαρτί όπου έχουμε σχεδιάσει το αντίστοιχο διάγραμμα τοποθετούμε ένα άλλο φύλλο χάρτου χωρισμένο σε τετραγωνίδια. Κάθε τετράγωνο έχει πλευρά, συνήθως, ίση με το 1/10 της διαμέτρου του κύκλου του δικτύου Schmidt που χρησιμοποιούμε (Σχ. Κ.25).
Πολλές φορές εν τούτοις, η εκλογή του μεγέθους της πλευράς των τετραγωνιδίων αυτών, εξαρτάται και από το συνολικό αριθμό των πόλων που προβάλλονται, καθώς και της εμφανιζόμενης πυκνότητας κατά περιοχές.
- Μετρούμε τους πόλους που περικλείονται μέσα σε κάθε τετράγωνο και γράφουμε τον αριθμό τους στο κέντρο του αντίστοιχου τετράγωνου (Σχ. Κ.25).
- Για να έχουμε πληρέστερη απόδοση του επιδιωκούμενου σκοπού, μετατοπίζουμε το χαρτί με τα τετραγωνίδια με τέτοιον τρόπο, ώστε το κέντρο κάθε τετραγωνιδίου, να συμπέσει με το σημείο που κατείχε πριν τη μετακίνηση, μια κορυφή του.
Τον αριθμό των πόλων που περικλείονται σε κάθε νέο τετράγωνο, τον σημειώνουμε για άλλη μια φορά στο κέντρο του (Σχ. Κ.25).
- Στη συνέχεια, χαράσσουμε τις ισόπυκνες καμπύλες, έτσι ώστε αυτές να συνδέουν μεταξύ τους ίδιους αριθμούς και να περικλείουν μέσα τους αριθμούς μεγαλύτερους από αυτούς που ενώνουν.
Η σύνδεση ομάδων όμοιων αριθμών, γίνεται κατ' εκτίμηση (Σχ. Κ.25).
Με τον τρόπο αυτόν, καθορίζουμε περιοχές ή ζώνες με την ίδια πυκνότητα πόλων και κατ' επέκταση το σημείο της μεγαλύτερης συγκέντρωσης πόλων, που θα συμπίπτει, προφανώς, με το πεδίο, που περικλείει τον μέγιστο αριθμό πόλων.
- Για την καλλίτερη απόδοση του διαγράμματος χρησιμοποιούμε διάφορους χρωματισμούς ή γραμμικούς συμβολισμούς για κάθε ισόπυκνη επιφάνεια (Σχ. Κ.25).
Τα σύμβολα ή τα χρώματα αυτά, αναγράφονται δίπλα στο αντίστοιχο διάγραμμα με την επί τοις εκατό πυκνότητα κάθε ζώνης ή περιοχής. Για τον υπολογισμό της επί τοις εκατό πυκνότητας κάθε ζώνης λαμβάνονται υπόψη, το σύνολο των μετρήσεων και ο αριθμός των πόλων που περικλείονται από κάθε ισόπυκνη καμπύλη. Π.χ. στο συγκεκριμένο παράδειγμα που αναφέρεται το Σχ. Κ.25, επί συνόλου 100 μετρήσεων (δεν χρειάζεται προφανώς αναγωγή) έχουν σχεδιασθεί πεδία με πυκνότητες από 0%-2%, 2%-5%, 5%-9% και > 9%.
Τέλος δίπλα από κάθε τέτοιο διάγραμμα πυκνοτήτων επιβάλλεται να αναγράφεται, ο συνολικός αριθμός μετρήσεων που πραγματοποιήθηκε για να γίνει το διάγραμμα, καθώς και το είδος των τεκτονικών στοιχείων που απεικονίζονται (π.χ. 72 Β-άξονες πτυχών κ.ο.κ.).
 |
Σχ. Κ.25: Απεικόνιση των σταδίων εργασίας, για την εξακρίβωση των μέγιστων συγκέντρωσης τεκτονικών δομών, που προβάλλονται στο δίκτυο Schmidt με τη μορφή πόλων (C.T.H. 4. 1969). |
Κ. 2.2.5. Ανάλυση της αναπαράστασης των συνθηκών της τεκτονικής καταπόνησης με τη βοήθεια του δικτύου Schmidt - Μεταφορά
Με τη χρησιμοποίηση του δικτύου Schmidt, μπορούμε σε ορισμένες περιπτώσεις να υπολογίσουμε επακριβώς τη θέση που είχαν γεωλογικοί σχηματισμοί, πριν την τελευταία τους τεκτονική καταπόνηση.
Για την πραγματοποίηση μιας τέτοιας αναπαράστασης είναι απαραίτητο να διακρίνεται ευκρινώς η νεότερη υφή, οπότε τότε εφαρμόζεται η «μέθοδος της μεταφοράς».
Για τις μεταφορές, χρησιμοποιούνται οι πόλοι των επιπέδων ή γραμμώσεων, που αναπαριστάνουν τις αντίστοιχες τεκτονικές δομές στο διάγραμμα. Κατά τη διαδικασία της μεταφοράς τον πόλο ή τους πόλους της νεότερης υφής, τους μετατοπίζουμε στον Α-Δ άξονα του δικτύου, ενώ συγχρόνως, όλοι οι άλλοι πόλοι κινούνται με τις ίδιες γωνίες και την ίδια διεύθυνση πάνω στους παραλλήλους κύκλους του δικτύου.
Παρακάτω παραθέτουμε δυο παραδείγματα της διαδικασίας της μεταφοράς (αναπαράσταση της αρχικής δομής και θέσης των γεωλογικών σχηματισμών πριν την τελευταία τους τεκτονική καταπόνηση).
Ασβεστόλιθος του άνω Κρητιδικού με στοιχεία 150/65 ΒΑ, βρίσκεται με επικλυσιγενή ασυμφωνία πάνω σε σχηματισμούς του Δεβονίου με στοιχεία 4/75 ΒΔ (Σχ. Κ.26).
Τα στρώματα του Κρητιδικού, προφανώς, αποτέθηκαν οριζόντια. Η σημερινή τους τοποθέτηση οφείλεται, συνεπώς σε μια νέα μετακρητιδική τεκτονική καταπόνηση, η οποία επηρέασε, οπωσδήποτε και το υποκείμενο σύστημα του Δεβονίου.
Με βάση το παραπάνω γεγονός, για να
βρούμε την αρχική θέση των σχηματισμών του Δεβονίου, πριν την επίκλυση και
πριν τη μετακρητιδική τεκτονική καταπόνηση τους, εργαζόμαστε ως εξής:
Τον πόλο του κρητιδικού ασβεστόλιθου τον μετατοπίζουμε στον Α-Δ άξονα του
δικτύου και κατόπιν κατά την κλίση του (65°), επί του κέντρου του δικτύου
(Στη θέση αυτή έχουμε οριζοντιώσει τα κρητιδικά στρώματα).
Συγχρόνως, τη μετατόπιση αυτή ακολουθούν και οι δεβόνιοι σχηματισμοί, ο
πόλος των οποίων κινείται έτσι, με την ίδια γωνία κλίσεως και την ίδια
διεύθυνση (προς τα δεξιά), πάνω στον αντίστοιχο παράλληλο κύκλο (Σχ. Κ.26).
Επειδή κατά την κίνηση αυτή ο πόλος του Δεβονίου υπερβαίνει την περιφέρεια,
αυτός θα εμφανισθεί στο απέναντι τεταρτημόριο και στον συμμετρικό παράλληλο
κύκλο από αυτόν που βρίσκονταν (Σχ. Κ.26).
Η καινούργια θέση του πόλου (Ρι΄) των Δεβόνιων στρωμάτων, μας δίδει προφανώς
και τα στοιχεία της προ- κρητιδικής θέσης τους (14/50 ΝΑ, Σχ. Κ.26).
Σε λιθανθρακοφόρα στρώματα με στοιχεία 56/50 ΒΔ εντοπίσθηκαν συνιζηματογενή ρήγματα με διάταξη 124/58 ΝΔ.
Επειδή τα συνιζηματογενή ρήγματα δημιουργούνται κατά το στάδιο της απόθεσης των ιζημάτων (βλ. κεφ. ρήγματα-διακλάσεις), όταν αυτά δηλαδή βρίσκονται στην οριζόντια θέση, για να βρούμε τον προσανατολισμό των ρηγμάτων, κατά τον χρόνο γένεσης τους, θα πρέπει να οριζοντιώσουμε τα λιθανθρακοφόρα στρώματα.
Ακολουθώντας έτσι, την ίδια πορεία εργασίας (μεταφοράς), με το προηγούμενο παράδειγμα, βρίσκουμε την πρωταρχική θέση των συνιζημα-τογενών ρηγμάτων που είναι Pt = 108/84 ΝΔ (Σχ. Κ.27).
Η «μέθοδος της μεταφοράς» όπως φαίνεται λοιπόν, αποτελεί ένα σημαντικό βοήθημα της τεκτονικής ανάλυσης μιας περιοχής και πολλές φορές θα πρέπει να την εφαρμόσουμε, για να δώσουμε απάντηση σε προβλήματα που θα μας απασχολήσουν. Όπως π.χ. στην εξακρίβωση της σχετικής ηλικίας μιας γράμμωσης, που βρίσκεται πάνω στις πτέρυγες μιας πτυχής, ως προς την πτυχή την ίδια κ.ά.
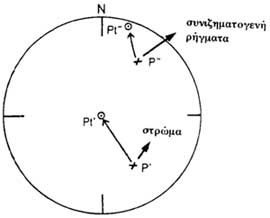 |
| Σχ. Κ.27: Μεταφορά επιφανειακών στοιχείων στο δίκτυο Schmidt. (C.T.H. 4, 1969). |
Έτσι, όταν μετά την οριζοντίωση των πτερύγων της πτυχής (σύμφωνα με τη διαδικασία που περιγράψαμε), οι γραμμώσεις που προκύπτουν είναι παράλληλες μεταξύ τους, τότε η γράμμωση είναι παλιότερη της πτυχής. Αντίθετα στην περίπτωση που δεν είναι παράλληλες, τότε η γράμμωση είναι νεότερη, από την πτυχή (Σχ. Κ.28) (βλ. κεφ. πτυχές, επαναπτύχωση).
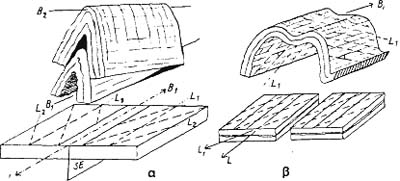 |
| Σχ. Κ.28: α) Η γράμμωση (L2) είναι νεότερη από την πτυχή (Β1, L1). β) Η γράμμωση (L1) είναι παλιότερη της πτυχής (B.L). (Metz. 1967). |
Κ. 2.2.6. Μελέτη της γεωμετρίας των στοιχείων της υφής με τη βοήθεια των διαγραμμάτων Schmidt
Στα προηγούμενα κεφάλαια περιγράφηκαν οι βασικές αρχές της χρήσης του δικτύου Schmidt, καθώς και οι τρόποι της απεικόνισης ή της προβολής γραμμικών και επιφανειακών στοιχείων στο δίκτυο Schmidt. Στα επόμενα θα δειχθεί, πως παριστάνονται στο δίκτυο ορισμένες βασικές τεκτονικές δομές (πτυχές, διακλάσεις κλπ) και πως διατάσσονται αυτές, σ' ένα διάγραμμα Schmidt, εφ΄ όσον ανήκουν στο ίδιο τεκτονικό γεγονός.
Κ. 2.2.6.1. Η πτυχή στο διάγραμμα Schmidt
Για τις μορφές των πτυχών, που αναπαρίστανται στα επόμενα παραδείγματα, ισχύει ο περιορισμός, ότι χαρακτηρίζονται από ρομβική συμμετρία και αποτελούν κυλινδρικές πτυχές. Αυτό σημαίνει ότι οι άξονες a,b.c του τριαξονικού συστήματος αναφοράς λαμβάνονται, κατά συνθήκη, κάθετοι μεταξύ τους.
Σε περιπτώσεις μονοκλινών πτυχών, είναι δυνατόν να μετατρέψουμε τη μονοκλινή συμμετρία τους σε ρομβική δια της χρησιμοποίησης ενός βοηθητικού άξονα a' ή c', κάθετου στην αξονική επιφάνεια της πτυχής (Σχ. Κ.29), έτσι ώστε η πτυχή να εμφανίζεται ως ρομβική (βλ. κεφ. πτυχές).
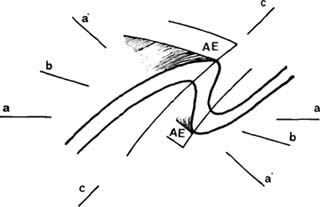 |
| Σχ. Κ.29: Μετατροπή μιας μονοκλινής συμμετρίας πτυχής, σε ρομβικής συμμετρίας. |
Άξονας πτυχής
Στην περίπτωση που η μέτρηση του άξονα της πτυχής μπορεί να γίνει απ' ευθείας με τη γεωλογική πυξίδα, τότε με βάση τα στοιχεία που θα μετρηθούν, είναι δυνατόν να αναπαρασταθεί αυτός στο δίκτυο Schmidt, ως γραμμικό στοιχείο με τη μορφή πόλου. Ο πόλος του άξονα της πτυχής συμβολίζεται στο διάγραμμα Schmidt με το γράμμα Β.
Στις περιπτώσεις που είναι αδύνατη η απευθείας μέτρηση του Β-άξονα της πτυχής, τότε τα στοιχεία αυτού είναι δυνατόν να υπολογισθούν εμμέσως ως εξής:
1) Δια μετρήσεως των στοιχείων και των δυο πτερύγων της πτυχής. Η γραμμή της τομής των δυο αυτών ομοειδών επιπέδων (β-άξονας), ταυτίζεται με τον άξονα της πτυχής. Ο πόλος της γραμμής αυτής ταυτίζεται συνεπώς με το Β σημείο και συμβολίζεται με το γράμμα β. Έχουμε συνεπώς β = Β (Σχ. Κ. 30α).
2) Δια μετρήσεως των στοιχείων της μιας πτέρυγας της πτυχής και της επιφανείας σχιστότητας της πτυχής κατά αξονικό επίπεδο. Εφόσον το επίπεδο της πτέρυγας της πτυχής πρόκειται για ss-επιφάνεια η γραμμή τομής των δυο παραπάνω ετεροειδών επιφανειών, χαρακτηρίζεται ως δ-άξονας και συμπίπτει με τη διεύθυνση του άξονα της πτυχής (βλ. κεφ. γραμμώσεων). Ο πόλος συνεπώς του δ-άξονα στο διάγραμμα Schmidt, θα ταυτίζεται με τα σημεία Β και β. Έχουμε συνεπώς Β = β = δ (Σχ. Κ.30γ).
Εφόσον το επίπεδο των πτερύγων της πτυχής, πρόκειται για s-επιφάνεια, τότε θα έχουμε στην περίπτωση αυτή τομή δυο ομοειδών επιφανειών και στην πραγματικότητα ένα β-άξονα, ο οποίος θα συμπίπτει, επίσης με τον Β-άξονα της πτυχής (Σχ. Κ.30β).
Για τον υπολογισμό λοιπόν, εμμέσως του Β-άξονα της πτυχής, σύμφωνα με τις δυο παραπάνω περιπτώσεις (1 και 2), θα πρέπει σε κάθε περίπτωση, να προβάλλουμε στο δίκτυο Schmidt ανά δύο τις ανάλογες επιφάνειες, υπό μορφή μεγίστων κύκλων (ss1/ss2, ss/s και s1/s2). Στο διάγραμμα το σημείο τομής των μεγίστων κύκλων των επιφανειών αυτών, θα μας δώσει τα στοιχεία του ζητούμενου Β-άξονα της πτυχής.
Προφανώς οι μετρήσεις που θα αντιστοιχούν σε κάθε ζεύγος επιφανειών που περιγράψαμε μπορεί, ανάλογα να είναι περισσότερες από μια για κάθε επιφάνεια του ζεύγους (Σχ. Κ.30 και Σχ. Κ.31
Είναι δυνατόν όμως, τα στοιχεία των επιφανειών που αναφέραμε, λαμβανόμενα πάντα ανά ζεύγη, όπως τα περιγράψαμε, να προβληθούν στο δίκτυο Schmidt, υπό μορφή πόλων (Σχ. Κ.32).
Στην προκειμένη περίπτωση, για τον υπολογισμό του Β-άξονα φέρουμε τον μεσημβρινό του δικτύου, ο οποίος διέρχεται από τους πόλους ή από τα δυο μέγιστα συγκεντρώσεων, των πόλων των επιφανειών που προβάλλαμε (Προφανώς οι πόλοι αυτοί θα βρίσκονται διεσπαρμένοι πάνω σε μια ζώνη, ή ανάλογα συγκεντρωμένοι σε δυο σημεία του δικτύου, Σχ. Κ.32).
Ο μεσημβρινός αυτός καλείται π-κύκλος. Ο πόλος του π-κύκλου, χαρακτηρίζεται ως π-πόλος και συμπίπτει με τον ζητούμενο Β-άξονα της πτυχής (Σχ. Κ.32).
Σ' ένα γενικευμένο σχήμα ισχύει συνεπώς η σχέση:
π-πόλος = βss1/βss2 = βs1/βs2 = δss/s = Β-άξονας
Έτσι λοιπόν αρκεί να κατασκευάσουμε στο δίκτυο Schmidt, κάποιο από τα τρία παραπάνω σημεία για να βρούμε με ακρίβεια τα στοιχεία του Β-άξονα.
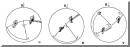 |
Σχ. Κ.32: Εξακρίβωση του Β-άξονα, από την προβολή των στοιχείων των πτερύγων της πτυχής, με τη μορφή πόλων (Κίλιας, 1980). |
Απεικόνιση μορφών πτυχών στο δίκτυο Schmidt με τη χρησιμοποίηση μεγίστων κύκλων.
Προβάλλοντας στο δίκτυο Schmidt τα στοιχεία (παράταξη, διεύθυνση κλίσης και γωνία κλίσης) των πτερύγων μιας πτυχής με τη μορφή μεγίστων κύκλων, είμαστε σε θέση από τον τρόπο διάταξης των μεγίστων κύκλων να κατανοήσουμε και να χαρακτηρίσουμε τόσο τη μορφή της πτυχής, όσο και τα στοιχεία συμμετρίας αυτής. Δεν μπορούμε να διακρίνουμε όμως, εάν στο αντίστοιχο διάγραμμα απεικονίζεται η συγκλινική ή η αντικλινική δομή της πτυχής.
Το τελευταίο αποτελεί, βέβαια, μικρής σημασίας γεγονός για την τεκτονική ανάλυση μιας περιοχής, αφού οι συνθήκες συμμετρίας της πτυχής είναι οι ίδιες, είτε αυτές εξετάζονται στο συγκλινικό της μέρος, είτε στο αντικλινικό της.
Εν τούτοις για την καλλίτερη απόδοση των διαγραμμάτων θα πρέπει κατά την υπαίθρια εργασία μας να σημειώνουμε σε ποιο μέρος της πτυχής (αντίκλινο ή σύγκλινο) πραγματοποιήσαμε τις μετρήσεις και τις παρατηρήσεις μας.
Στο σχήμα Κ.33, δίνονται ορισμένα χαρακτηριστικά παραδείγματα μορφών πτυχών σε διαγράμματα Schmidt.
Απεικόνιση μορφών πτυχών στο δίκτυο Schmidt με τη χρησιμοποίηση μόνο πόλων.
Το διάγραμμα που προκύπτει από την αναπαράσταση των πτυχών με τη χρησιμοποίηση μεγίστων κύκλων είναι πολύπλοκο και η προβολή πολλών στοιχείων μέτρησης προκαλεί πολλές φορές σύγχυση και ίσως αδυναμία κατασκευής του ίδιου του διαγράμματος. Για το λόγο αυτό προτιμάται συνήθως η απεικόνιση των πτυχών σε διαγράμματα Schmidt με τη χρησιμοποίηση πόλων.
Τα σχήματα Κ.34 και Κ.35 απεικονίζουν μια σειρά πτυχών, που προέκυψαν από την προβολή στο δίκτυο Schmidt με τη μορφή πόλων, των στοιχείων των πτερύγων τους.
Από τα σχήματα Κ.33, Κ.34 και Κ.35 συμπεραίνουμε, σε γενικές γραμμές ότι πτυχές με οριζόντιους Β-άξονες, απεικονίζονται με τους πόλους των Β-αξόνων τοποθετημένους σε δυο σημεία συμμετρικά αντίθετα ως προς το κέντρο του κύκλου και επάνω στην περιφέρεια του διαγράμματος.
Αντίθετα ο Β-πόλος κεκλιμμένων αξόνων πτυχών, εμφανίζεται ανάλογα σ' ένα μόνο μέρος μέσα στον κύκλο του διαγράμματος.
Εξ άλλου οι μέγιστοι κύκλοι ή τα μέγιστα συγκεντρώσεων των πόλων πτυχών με την ίδια κλίση πτερύγων, κατανέμονται συμμετρικά ως προς το κέντρο του κύκλου, ενώ αντίθετα σε πτυχές με απόκλιση (φορά) ασύμμετρα.
Στην τελευταία περίπτωση ανάλογα με την τοποθέτηση των μεγίστων, κύκλων ή των μεγίστων συγκεντρώσεων των πόλων μπορούμε να υποθέσουμε τη φορά της πτυχής.
Η γωνιακή απόσταση επίσης, μεταξύ των μεγίστων συγκεντρώσεων των πόλων, μας δίδει με ακρίβεια τη γωνία ανοίγματος (2α) των πτερύγων της πτυχής.
Καθορισμός της αξονικής επιφάνειας πτυχών από το διάγραμμα Schmidt.
Η αξονική επιφάνεια στο μεγαλύτερο μέρος των πτυχών διχοτομεί ως γνωστό τη δίεδρη γωνία ανοίγματος αυτών. Εξαίρεση αποτελεί η περίπτωση των ανισοπαχών πτυχών. Και στην περίπτωση αυτή όμως το νοητό επίπεδο που διχοτομεί τη γωνία ανοίγματος της πτυχής (μεσαίο επίπεδο) και η πραγματική αξονική επιφάνεια σχηματίζουν μικρή γωνία μεταξύ τους, έτσι ώστε σ' ένα γενικευμένο σχήμα, οι δυο αυτές επιφάνειες να θεωρείται ότι ταυτίζονται.
Επειδή εξ' άλλου κατά τη μελέτη της «ανάλυσης της υφής» μιας περιοχής η μικρή αυτή διαφορά της μεσαίας και της πραγματικής αξονικής επιφάνειας δεν παίζει σημαντικό ρόλο, για τον καθορισμό της αξονικής επιφάνειας πτυχών από τα διαγράμματα Schmidt, αρκεί να φέρουμε το επίπεδο που διχοτομεί τη γωνία ανοίγματος της πτυχής που απεικονίζεται στο διάγραμμα.
Για το σκοπό αυτό φέρουμε τον π-κύκλο της πτυχής κατά τα γνωστά. Στη συνέχεια φέρουμε τους δυο μέγιστους κύκλους που έχουν ως πόλους τα δυο μέγιστα συγκεντρώσεων των πόλων των πτερύγων της πτυχής. Πάνω στον π-κύκλο και στο μέσον της γωνιακής απόστασης των δυο μεγίστων κύκλων, σημειώνουμε ένα σημείο. Είναι φανερό ότι ο μέγιστος κύκλος που διέρχεται από το σημείο αυτό και τον Β-πόλο (πόλος του άξονα της πτυχής) παριστάνει τον ζητούμενο μέγιστο κύκλο της αξονικής επιφάνειας, αφού διχοτομεί τη γωνία ανοίγματος της πτυχής (Σχ. Κ.36). Για να φέρουμε αυτόν τον μέγιστο κύκλο, τοποθετούμε τα δυο σημεία (σημείο 292 που διχοτομεί τη γωνιακή απόσταση των δυο μεγίστου κύκλων και Β-πόλος), σ' ένα μεσημβρινό του δικτύου και σημειώνουμε τον μεσημβρινό αυτόν (Σχ. Κ.36).
Η διεύθυνση κλίσης της αξονικής επιφάνειας, η οποία εξάγεται από τη θέση του μεγίστου κύκλου της στο διάγραμμα, μας πληροφορεί για τη φορά της πτυχής. Η φορά της πτυχής, σε γενικές γραμμές, είναι αντίθετη της διεύθυνσης κλίσης της αξονικής επιφάνειας.
Η μεθοδολογία που περιγράψαμε εφαρμόζεται γενικά σε κάθε περίπτωση που θέλουμε να προσδιορίσουμε τη διχοτόμο δυο τυχόντων επιπέδων ή και γραμμώσεων ακόμη (Σχ. Κ.37).
Κ. 2.2.6.2. Καθορισμός της θέσης στο χώρο, των συντεταγμένων a-, b-, c του ορθογώνιου τριαξονικού συστήματος αναφοράς από τη μορφή της πτυχής, σε διαγράμματα Schmidt
Η τοποθέτηση στο χώρο του τριαξονικού συστήματος συντεταγμένων, σύμφωνα με τη μορφή της ανάλογης τεκτονικής δομής, μας βοηθάει στην ανάλυση της κινητικής και δυναμικής εικόνας μιας περιοχής.
Η διάταξη των συντεταγμένων a-, b-, c- του συστήματος, εκλέγεται έτσι, ώστε αυτές να ταυτίζονται με τις διευθύνσεις των τριών κύριων αξόνων της ελλειψοειδούς παραμόρφωσης (βλ. κεφ. ελλειψοειδής παραμόρφωση).
Το παραπάνω σύστημα αναφοράς είναι
μετατρέψιμο. Έτσι ανάλογα των συνθηκών μπορούμε να τοποθετήσουμε:
α) τους τρεις άξονες a-, b-. c- κάθετα μεταξύ τους, οπότε μιλάμε για ρομβική
συμμετρία,
β) τους δυο άξονες π.χ. τους a-, b-. κάθετα μεταξύ τους και τον τρίτο c- πλάγια
ως προς τους δυο άλλους, οπότε μιλάμε για μονοκλινή συμμετρία και,
γ) τους τρεις άξονες a-, b- c- υπό τυχαία γωνία μεταξύ τους, οπότε μιλάμε για
τρίκλινη συμμετρία (βλ. κεφ. πτυχών).
Συνήθως ο άξονας a- του τριαξονικού συστήματος συντεταγμένων παριστάνει τη διεύθυνση τη κύριας τεκτονικής κίνησης, που προκάλεσε την αντίστοιχη τεκτονική δομή. Ο b-άξονας συμπίπτει με τη διεύθυνση του άξονα παραμόρφωσης και συνεπώς είναι παράλληλος πάντοτε με τον Β-άξονα (άξονας πτυχής ή διάτμησης). Τέλος ο c-άξονας δείχνει τη διεύθυνση παραμόρφωσης του γεωλογικού σχηματισμού κατά το ύψος (Σχ. Κ.38).
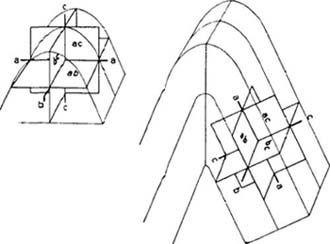 |
| Σχ. Κ.38: Τοποθέτηση των a-, b-, c- αξόνων υφής και των τριών κύριων επιπέδων που ορίζουν (ab, bc και ac), σε πτυχωσιγενείς δομές (C.T.H. 4, 1969). |
Σύμφωνα με τα παραπάνω γίνεται φανερό λοιπόν γιατί η τοποθέτηση των τριών αυτών αξόνων βοηθάει σε μεγάλο βαθμό στην επίλυση σημαντικών προβλημάτων της κινητικής και δυναμικής ανάλυσης μιας περιοχής.
Οι πτυχωσιγενείς δομές αποτελούν, όπως τονίσαμε, τις πιο χαρακτηριστικές τεκτονικές δομές για την ανεύρεση της θέσης του τριαξονικού συστήματος συντεταγμένων, αφού ο Β-άξονας της πτυχής συμπίπτει όπως τονίσαμε με το b-άξονα του συστήματος, ο a-άξονας συμπίπτει με τη διεύθυνση της συρρικνωτικής κίνησης κατά το οριζόντιο κυρίως επίπεδο και ο c-άξονας συμπίπτει με την καθ' ύψος παραμόρφωση του γεωλογικού σχηματισμού (βλ. κεφ. πτυχών).
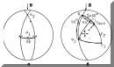
Για τον καθορισμό του τριαξονικού συστήματος συντεταγμένων με τη βοήθεια των διαγραμμάτων Schmidt εργαζόμαστε ως εξής: (Σχ. Κ.39).
 |
| Σχ. Κ.39: Τοποθέτηση των a-, b-, c- αξόνων υφής σε διάφορες μορφές πτυχών, με τη χρησιμοποίηση διαγραμμάτων Schmidt. Οι διακεκομμένοι με τις μικρές γραμμές μέγιστοι κύκλοι, παριστάνουν τις αξονικές επιφάνειες. Απεικονίζονται επίσης οι θέσεις των τριών κύριων επιπέδων (ab, bc και ac) (C.T.H. 4, 1969). |
- Υπό μορφή πόλων προβάλλουμε στο δίκτυο Schmidt τα
στοιχεία των πτερύγων μιας συγκεκριμένης ομάδας πτυχών.
- Φέρουμε τον π-κύκλο και τον π-πόλο, ο οποίος όπως τονίσαμε συμπίπτει με τον
Β-άξονα της πτυχής. Το σημείο αυτό θα δείχνει προφανώς και τη θέση του b-άξονα
του τριαξονικού συστήματος συντεταγμένων.
- Σημειώνουμε κατά τα γνωστά τους μέγιστους κύκλους των πόλων των στοιχείων των
πτερύγων της ομάδας πτυχών που μελετάμε. Στο μέσο της μικρότερης γωνιακής
απόστασης αυτών των μεγίστων κύκλων και πάνω στον π-κύκλο βρίσκεται ο c-άξονας.
- Περιστρέφουμε το δίκτυο Schmidt έτσι ώστε, ο π-κύκλος να συμπέσει με κάποιο
μεσημβρινό του δικτύου. Από τη θέση αυτή, σε απόσταση 90° από τον c-άξονα και
πάνω στον π-κύκλο βρίσκεται ο a-άξονας, ο οποίος θα δείχνει και τη διεύθυνση της
κύριας κίνησης που δημιούργησε τις αντίστοιχες πτυχωσιγενείς δομές (Σχ. Κ. 39).
Οι μέγιστοι κύκλοι που διέρχονται από τα σημεία a,b,c, θα παριστάνουν προφανώς τους μέγιστους κύκλους τριών επιπέδων που διέρχονται από τους άξονες a-, b-, c- του τριαξονικού συστήματος και είναι κάθετα μεταξύ τους (Σχ. Κ.38 και Κ.39).
Έτσι:
Ο bc- μέγιστος κύκλος θα χαρακτηρίζει το bc- επίπεδο το οποίο διέρχεται από τους b-, c-άξονες και είναι κάθετο στον a-άξονα. Το σημείο a θα παριστάνει συνεπώς τον πόλο του bc-επιπέδου.
Ο ac- μέγιστος κύκλος, που συμπίπτει και με τον π-κύκλο, θα χαρακτηρίζει το ac-επίπεδο, το οποίο διέρχεται από τους a-, c-άξονες και είναι κάθετο στον b-άξονα. Το σημείο b θα αποτελεί συνεπώς τον πόλο του ac-επιπέδου.
Ο ab-μέγιστος κύκλος θα παριστάνει το ab-επίπεδο, το οποίο διέρχεται από τους a-, b-άξονες και είναι κάθετο στον c-άξονα. Το σημείο c θα συμπίπτει συνεπώς με τον πόλο του ab-επιπέδου.
Κάθε άλλο επίπεδο το οποίο τέμνει σε τυχαία θέση τους τρεις άξονες του τριαξονικού συστήματος συντεταγμένων θα χαρακτηρίζεται ως hkl• επίπεδο. Το γράμμα h δείχνει τη θέση του επιπέδου ως προς τον a-άξονα, το k δείχνει τη θέση του επιπέδου ως προς τον b-άξονα, ενώ το l δείχνει τη θέση του επιπέδου ως προς τον c-άξονα.
Έτσι κάποιο επίπεδο παράλληλο σ' ένα μόνο από τους άξονες του τριαξονικού συστήματος συντεταγμένων θα χαρακτηρίζεται ανάλογα, ως 0kl-, h0l-, hk0-επίπεδο, όταν βρίσκεται αντίστοιχα παράλληλο στον a-, b- και c-άξονα (Σχ. Κ.40).
Η θέση των τριών τελευταίων επιπέδων στα διαγράμματα Schmidt απεικονίζονται στα Σχ. Κ.42, Κ.43, Κ.44.
Κ. 2.2.6.3. Οι ρηξιγενείς δομές στο δίκτυο Schmidt
Οι ρηξιγενείς δομές μιας περιοχής (ρήγματα, διακλάσεις), εφόσον ανήκουν στον ευρύτερο κύκλο των γεγονότων μιας συγκεκριμένης πτυχογόνου παραμορφωτικής φάσης, θα τοποθετηθούν με απόλυτη συμμετρία και κατά καθορισμένο τρόπο ως προς τις δομές αυτής της πτυχογόνου τεκτονικής.
Αυτές θα παριστάνουν ac-, bc-, ab-επιφάνειες ή 0kl-, h0l και hk0- επιφάνειες ως προς τα στοιχεία συμμετρίας (a-, b-, c- άξονες) των πτυχών της συγκεκριμένης φάσης, θα βρίσκονται συνεπώς παράλληλα και κάθετα ως προς τα ac-, bc-, ab- επίπεδα ή ως προς τους a-, b- και c-άξονες του τριαξονικού συστήματος συντεταγμένων.
Από το σύνολο συνεπώς των ρηξιγενών δομών μιας περιοχής οι ac-, bc- και ab- ρηξιγενείς δομές βρίσκονται πάντοτε ανάλογα παράλληλα προς δυο άξονες του τριαξονικού συστήματος συντεταγμένων και εμφανίζονται μεμονωμένες. Οι 0hk-, h0l- και hk0- ρηξιγενείς δομές βρίσκονται παράλληλα ως προς ένα άξονα, του τριαξονικού συστήματος συντεταγμένων και εμφανίζονται κατά ζεύγη, με την αυτή παράταξη, αλλά αντίθετη διεύθυνση κλίσης (Σχ. Κ.40). Από αυτές, όπως αναφέρθηκε, οι πρώτες χαρακτηρίζονται ως ρηξιγενείς δομές θραύσης, ενώ οι δεύτερες ως διατμητικές ρηξιγενείς δομές (βλ. κεφ. ρήγματα-διακλάσεις).
Η σχέση συνεπώς των ρηξιγενών δομών ως προς κάποιο τριαξονικό σύστημα συντεταγμένων, που τοποθετήθηκε με βάση τις μορφές μιας πτυχογόνου τεκτονικής, παίζει καθοριστικό παράγοντα στη γεωμετρική και γενετική ταξινόμηση αυτών. Γεγονός οπωσδήποτε βασικό για την εξακρίβωση των τεκτονικών κινήσεων και δυνάμεων που έδρασαν σε κάποια περιοχή και δημιούργησαν την ανάλογη τεκτονική δομή της.
Για να καθορίσουμε λοιπόν το είδος των ρηξιγενών δομών, αρκεί να τις προβάλλουμε υπό μορφή πόλων ή μεγίστων κύκλων στο δίκτυο Schmidt. Η θέση των πόλων ή μεγίστων κύκλων των επιφανειών αυτών σε σχέση με τη θέση των a-, b-, c-αξόνων, θα χαρακτηρίσει και τις ρηξιγενείς αυτές δομές.
Έτσι σύμφωνα με όλα τα παραπάνω:
α) Οι ρηξιγενείς δομές, οι πόλοι των οποίων συγκεντρώνονται γύρω από τον πόλο
του b-άξονα, θα χαρακτηρίζονται ως ac-δομές, αφού ο μέγιστος κύκλος τους
συμπίπτει με τον μέγιστο κύκλο του ac-επιπέδου (Σχ. Κ.41).
β) Οι ρηξιγενείς δομές, οι πόλοι των οποίων
συγκεντρώνονται γύρω από τον πόλο του a-άξονα, θα χαρακτηρίζονται ως bc-δομές,
αφού ο μέγιστος κύκλος τους συμπίπτει με τον μέγιστο κύκλο του bc-επιπέδου (Σχ.
Κ.41).
γ) Οι ρηξιγενείς δομές, οι πόλοι των οποίων συγκεντρώνονται γύρω από τον πόλο
του c-άξονα, θα χαρακτηρίζονται ως ab-δομές, αφού ο μέγιστος κύκλος τους
συμπίπτει με τον μέγιστο κύκλο του ab-επιπέδου (Σχ. Κ.41).
δ) Οι πόλοι των h0l- ρηξιγενών δομών θα συγκεντρώνονται πάνω στον π-κύκλο ή στον ac-μέγιστο κύκλο, αφού οι ρηξιγενείς αυτές δομές βρίσκονται παράλληλα στον b-άξονα (Σχ. Κ.42).
ε) Οι πόλοι των hk0-ρηξιγενών δομών θα βρίσκονται πάνω στον ab-μέγιστο κύκλο, αφού οι ρηξιγενείς αυτές δομές είναι παράλληλες στον c-άξονα (Σχ. Κ.43).
στ) Τέλος οι ρηξιγενείς δομές, οι πόλοι των οποίων συγκεντρώνονται πάνω στον bc-μέγιστο κύκλο, θα χαρακτηρίζονται ως 0kl-ρηξιγενείς δομές, αφού θα βρίσκονται παράλληλα στον a-άξονα (Σχ. Κ.44).
 |
Σχ. Κ.44: Απεικόνιση ορισμένων μορφών πτυχών με τους a-, b-, c- άξονες υφής και τις 0kl-ρηξιγενείς επιφάνειες (διατμητικές ρηξιγενείς δομές) (C.T.H. 4, 1969). (Συμβολισμοί κεφ. Κ. 2.2. 7). |
Αντίστροφα εξετάζοντας το όλο θέμα, μπορούμε να τοποθετήσουμε τους a-, b-, c- άξονες του τριαξονικού συστήματος συντεταγμένων, από τη θέση των πόλων ρηξιγενών δομών που έχουν ήδη χαρακτηρισθεί.
Έτσι π.χ. οι πόλοι των ac-, bc- και ab- ρηξιγενών δομών θα δίδουν συγχρόνως αντίστοιχα και τους πόλους των b-, a- και c- αξόνων του τριαξονικού συστήματος. Ενώ οι πόλοι των h0l-, 0kl- και hk0- ρηξιγενών δομών θα τοποθετούν αντίστοιχα τους ac- (π-κύκλο), bc- και ab- μέγιστους κύκλους και συνεπώς τους b-, a- και c- άξονες του τριαξονικού συστήματος συντεταγμένων.
Συνοψίζοντας όλα τα παραπάνω σ' ένα γενικευμένο σχήμα, είναι δυνατόν να δώσουμε τις παρακάτω μεγάλης σημασίας σχέσεις συμμετρίας της τεκτονικής δομής μιας περιοχής (Σχ. Κ.45 και Σχ. Κ.46).
b = - Σημείο τομής των μεγίστων κύκλων των
h0l-ρηξιγενών επιφανειών.
- Πόλος του μεγίστου κύκλου, που προκύπτει από τα μέγιστα
συγκέντρωσης των πόλων των h0l - ρηξιγενών επιφανειών.
- Πόλος του μέγιστου κύκλου των ac-ρηξιγενών δομών.
- Σημείο τομής των μεγίστων κύκλων των ab- και bc-ρηξιγενών
δομών.
- Πόλος του μεγίστου κύκλου, που προκύπτει από τα μέγιστα
συγκεντρώσεως των πόλων των ab- και bc-ρηξιγενών δομών (π-κύκλος ή ac-μέγιστος
κύκλος).
c = - Σημείο τομής των μέγιστων κύκλων των hk0-
ρηξιγενών επιφανειών.
- Πόλος του μεγίστου κύκλου, που προκύπτει από τα μέγιστα
συγκέντρωσης των πόλων των hk0- ρηξιγενών επιφανειών.
- Πόλος του μεγίστου κύκλου των ab-ρηξιγενών δομών.
- Σημείο τομής των μέγιστων κύκλων των ac- και bc-ρηξιγενών
δομών.
- Πόλος του μεγίστου κύκλου, που προκύπτει από τα μέγιστα
συγκέντρωσης των πόλων των ac- και bc-ρηξιγενών δομών (ab-μέγιστος κύκλος)
a'/a = - Σημείο τομής των μέγιστων κύκλων των
0kl-ρηξιγενών επιφανειών.
- Πόλος του μέγιστου κύκλου που προκύπτει από τα μέγιστα
συγκεντρώσεως των πόλων των 0kl-ρηξιγενών δομών.
- Πόλος του μέγιστου κύκλου των bc-ρηξιγενών δομών.
- Σημείο τομής των μέγιστων κύκλων των ab- και ac-ρηξιγενών
δομών.
- Σημείο τομής του μέγιστου κύκλου, που προκύπτει από τα
μέγιστα συγκέντρωσης των πόλων των ab- και ac- ρηξιγενών δομών (bc-μέγιστος
κύκλος).
ac - μέγιστος κύκλος: Οι πόλοι των a- και c-αξόνων, καθώς και τα μέγιστα συγκέντρωσης των πόλων των h0l-ρηξιγενών επιφανειών βρίσκονται πάνω στον ίδιο μέγιστο κύκλο (ac-μέγιστος κύκλος ή π-κύκλος). Η γωνιακή απόσταση μεταξύ των a- και c- πόλων πάνω στον μέγιστο κύκλο ανέρχεται σε 90°. Η γωνία μεταξύ των μέγιστων συγκεντρώσεων των πόλων των h0l-ρηξιγενών δομών, διχοτομείται μια φορά από των a-άξονα και μια φορά από τον c-άξονα.
ab - μέγιστος κύκλος: Οι πόλοι των a- και b-αξόνων,
καθώς και τα μέγιστα συγκεντρώσεως των πόλων των hk0- ρηξιγενών επιφανειών
βρίσκονται πάνω στον ίδιο μέγιστο κύκλο (ab-μέγιστος κύκλος).
Η γωνιακή απόσταση μεταξύ των a- και b-πόλων πάνω στον μέγιστο κύκλο
ανέρχεται σε 90°. Η γωνία μεταξύ των μέγιστων συγκεντρώσεων των πόλων των
hk0-ρηξιγεvώv δομών διχοτομείται μια φορά από τον a- και μια φορά από τον
b-άξονα.
bc - μέγιστος κύκλος: Οι πόλοι των b-και c-αξόνων καθώς και τα μέγιστα συγκεντρώσεως των πόλων των 0kl-ρηξιγενών επιφανειών βρίσκονται πάνω στον ίδιο μέγιστο κύκλο (bc-μέγιστος κύκλος). Η γωνιακή απόσταση μεταξύ των c- και b-πόλων πάνω στον μέγιστο κύκλο ανέρχεται σε 90°. Η γωνία μεταξύ των μέγιστων συγκεντρώσεων των πόλων των 0kl-ρηξιγενών δομών, διχοτομείται μια φορά από τον b- και μια φορά από τον c-άξονα.
(Υπενθυμίζεται ότι οι h0l-, hk0- και 0kl- ρηξιγενείς δομές εμφανίζονται ως συζυγή συστήματα ρήξεων, σε αντίθεση με τις ac-, bc- και ab-ρηξιγενείς δομές που εμφανίζονται μεμονωμένες).
Κ. 2.2.6.4. Οι γραμμώσεις ολίσθησης στα διαγράμματα Schmidt
α. Μέτρηση και αναπαράσταση στο δίκτυο Schmidt, των στοιχείων των γραμμώσεων ολίσθησης:
Σε γενικές γραμμές, υπάρχουν δυο μέθοδοι μέτρησης των γραμμώσεων ολίσθησης.
α.1. Η κλασική μέθοδος μέτρησης γραμμικών στοιχείων με τη
γεωλογική πυξίδα (Σχ. Κ. 10).
α.2. Συχνά όμως ο τρόπος αυτός της μέτρησης γραμμικών στοιχείων δεν είναι
εφικτός. Στις περιπτώσεις αυτές, μετράμε τη γωνία που σχηματίζει η διεύθυνση της
γράμμωσης πάνω στην επιφάνεια, με την γραμμή παράταξης της επιφάνειας, που φέρει
τη γράμμωση (γωνία pitch ή rake). Επί πλέον καθορίζουμε και τη διεύθυνση βύθισης
του γραμμικού στοιχείου ως προς τη γραμμή παράταξης.
Στη συνέχεια για να μπορέσουμε να εξακριβώσουμε τα πραγματικά και ακριβή στοιχεία της γράμμωσης (παράταξη, διεύθυνση κλίσης και γωνία κλίσης), προβάλλουμε την επιφάνεια που φέρει τη γράμμωση στο δίκτυο Schmidt, με τη μορφή μεγίστου κύκλου (Σχ. Κ.47, Στοιχεία της επιφάνειας 135/60 ΝΔ).
Τέλος προσανατολίζουμε τον μέγιστο κύκλο της επιφάνειας στο Β-Ν άξονα του δικτύου, περιστρέφοντας αριστερόστροφα το δίκτυο κατά 135° (όση είναι η παράταξη της επιφάνειας). Στη θέση αυτή από την περιφέρεια προς το κέντρο και πάνω στον μέγιστο κύκλο μετράμε τόση γωνία, όση είναι η γωνία που σχηματίζει η γράμμωση πάνω στην επιφάνεια και η γραμμή παράταξης της επιφάνειας και σημειώνουμε τον πόλο της γράμμωσης (Σχ. Κ.47). Η διεύθυνση βύθισης της γράμμωσης μας δείχνει εάν θα μετρήσουμε από τον Β ή τον Ν.
Το σημείο αυτό που θα πάρουμε πάνω στον
μέγιστο κύκλο μας δίνει, προφανώς, με ακρίβεια και τα πραγματικά στοιχεία της
αντίστοιχης γράμμωσης.
Εκείνο που πρέπει να προσέξουμε είναι το σημείο του δικτύου (Β ή Ν) από το οποίο
θα αρχίσουμε να μετράμε την αντίστοιχη γωνία που υπολογίσαμε στο ύπαιθρο.
Αυτό θα εξαρτηθεί από τη διεύθυνση βύθισης της γράμμωσης ως προς τη γραμμή παράταξης. Στο παράδειγμα του Σχ. Κ.47, η επιφάνεια έχει στοιχεία 135/60 ΝΔ, η γωνία που σχηματίζει η γράμμωση πάνω στην επιφάνεια και η γραμμή παράταξης της επιφάνειας είναι 70°, ενώ η διεύθυνση βύθισης της γράμμωσης είναι ΒΔ. Τα στοιχεία συνεπώς της συγκεκριμένης γράμμωσης, υπολογίζονται σε 82/54 ΝΔ.
Αντίστροφα εξετάζοντας το όλο θέμα, είναι δυνατόν από τα στοιχεία δυο διαφορετικών γραμμών ολίσθησης πάνω σε μια επιφάνεια, να υπολογίσουμε επακριβώς τα στοιχεία της συγκεκριμένης επιφάνειας (παράταξη, διεύθυνση κλίσης και γωνία κλίσης). Αυτό θα γίνει, εάν προβάλλουμε στο δίκτυο Schmidt με τη μορφή πόλων, τα δυο αυτά γραμμικά στοιχεία. Ο μεσημβρινός που θα περνάει από τους δυο αυτούς πόλους θα παριστάνει τον μέγιστο κύκλο της ζητούμενης επιφάνειας (Σχ. Κ.47).
Ο υπολογισμός των στοιχείων των γραμμών ολίσθησης πάνω σε ρηξιγενείς επιφάνειες ή γενικά πάνω σε επιφάνειες ολίσθησης (ss- ή s-επιφάνειες), αποκτά ιδιαίτερη σημασία, από το γεγονός ότι με τον τρόπο αυτό είμαστε σε θέση να εξακριβώσουμε τις διευθύνσεις κινήσεων των τεμαχών εκατέρωθεν μιας επιφάνειας ολίσθησης.
Η όλη διεργασία λοιπόν που περιγράψαμε αποτελεί ένα πρώτο βήμα για την ερμηνεία της κινητικής και της δυναμικής της ρηξιγενής δομής που μελετάται, ή γενικά και της ευρύτερης περιοχής μελέτης.
β. Εύρεση του προσανατολισμού της τάσης στα ρήγματα:
Μπορούμε να διακρίνουμε τις εξής περιπτώσεις:
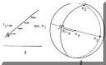
β.1. Όταν δίνεται συζυγές σύστημα ρηξιγενών επιφανειών (π.χ. h0l-, 0kl- ή hk0-ρηξιγενείς δομές) και είναι δυνατή η μέτρηση των στοιχείων των δυο τεμνομένων συνόλων των ρηξιγενών δομών, προβάλλουμε στο δίκτυο Schmidt με τη μορφή μεγίστων κύκλων τα δυο σύνολα των επιφανειών που σχηματίζονται (Σχ. Κ.48).
 |
Σχ. Κ.48: Εύρεση του προσανατολισμού των τάσεων στα ρήγματα, με τη χρησιμοποίηση τον δικτύου Schmidt. α) συζυγή ρήγματα, β) ρήγμα και γραμμές ολίσθησης (Ragan, 1968). |
Η τομή των δυο μεγίστων κύκλων μας δίνει τον πόλο του άξονα σ2 (b-άξονας, Β-άξονας διάτμησης). Ο πόλος του σ1-άξονα (διεύθυνση μέγιστης τάσης, a-άξονας), θα πρέπει να απέχει 90° από το σ2 και να διχοτομεί τη μικρότερη γωνία των δυο συνόλων των ρηξιγενών δομών. Βρίσκεται δηλαδή πάνω στον μεσημβρινό που διχοτομεί τη γωνία των δυο μέγιστων κύκλων των επιφανειών των ρηξιγενών δομών και σε απόσταση 90° από τον πόλο του σ2-άξονα (βλ. κεφ. ρήγματα-διακλάσεις και ελλειψοειδές παραμόρφωσης).
Ο πόλος του σ3-άξονα θα είναι ο πόλος του μέγιστου κύκλου σ1σ2, γιατί ως γνωστό απέχει από τους σ1 και σ2 άξονες 90° (Σχ. Κ.48).
β.2. Στην περίπτωση που δίδεται μόνο ένα ρήγμα (μεταπτωτικού, συνήθως χαρακτήρα) και γράμμωση ολίσθησης πάνω στην επιφάνεια του, ακολουθούμε τον εξής τρόπο εργασίας: (Η μέτρηση της γράμμωσης γίνεται με τον τρόπο που περιγράψαμε).
Προβάλλουμε με τη μορφή μεγίστου κύκλου την επιφάνεια του ρήγματος. Πάνω σ' αυτή και με τον τρόπο που ήδη περιγράψαμε, σημειώνουμε τον πόλο της γράμμωσης ολίσθησης.
Σε απόσταση 90° από τον πόλο της γράμμωσης και πάνω στον μέγιστο κύκλο της ρηξιγενής επιφάνειας θα βρίσκεται ο κύριος σ2-άξονας ενδιάμεσος άξονας ή (b-άξονας).
Οι άξονες σ1 και σ3 βρίσκονται σε απόσταση 90° από τον σ2-άξονα και συνεπώς, θα βρίσκονται πάνω στον μέγιστο κύκλο του σ2-πόλου. Πάνω σ' αυτόν τον μέγιστο κύκλο και σε απόσταση ~30° (όση δηλαδή υπολογίζεται για τα γεωλογικά σώματα η γωνία «εσωτερικής τριβής του υλικού», βλ. κεφ. ρήγματα-διακλάσεις) από τον πόλο της γράμμωσης ολίσθησης βρίσκεται ο πόλος του σ1-άξονα (διεύθυνση μεγίστης τάσης).
Σε απόσταση 90° από τον σ1-πόλο και πάνω στον ίδιο μέγιστο κύκλο βρίσκεται ο πόλος του σ3-άξονα (διεύθυνση ελάχιστης τάσης). (Σχ. Κ.48).
β.3. Στην περίπτωση που δίδεται το επίπεδο του ρήγματος και το επίπεδο των διακλάσεων εφελκυσμού, εργαζόμαστε με τον εξής τρόπο:
Προφανώς η τομή των μέγιστων κύκλων των δυο ρηξιγενών επιφανειών θα μας δίνει τον πόλο του σ2-άξονα. Πάνω στον μέγιστο κύκλο των διακλάσεων εφελκυσμού και σε απόσταση 90° από τον σ2-πόλο, θα βρίσκεται ο σ1-άξονας.
Ο πόλος του σ1σ2-μέγιστου κύκλου (μέγιστος κύκλος των διακλάσεων εφελκυσμού), θα δίνει προφανώς, τον σ3-άξονα. Πάνω στον μέγιστο κύκλο του ρήγματος και σε απόσταση 90° από τον σ2-πόλο, θα βρίσκεται ο πόλος D, της γράμμωσης ολίσθησης, που πιθανόν να σχηματίσθηκε κατά την κίνηση. Η γωνιακή απόσταση μεταξύ του D-πόλου και σ1-πόλου μας δίνει τη γωνία εσωτερικής τριβής του υλικού (Σχ. Κ.49).
 |
Σχ. Κ.49: Εύρεση του προσανατολισμού των τάσεων με βάση ένα ρήγμα και τις διακλάσεις εφελκυσμού, με τη χρησιμοποίηση του δικτύου Schmidt (Ragan 1968). |
Από όλα τα παραπάνω γίνεται φανερό, ότι η μέτρηση στο ύπαιθρο με τη γεωλογική πυξίδα, επιφανειών και γραμμικών στοιχείων (δομών) μιας περιοχής, η προβολή τους με τη μορφή μεγίστων κύκλων ή πόλων στο δίκτυο Schmidt, η στατιστική επεξεργασία και η σωστή αξιολόγηση των διαγραμμάτων που προκύπτουν, αποτελούν καθοριστικό παράγοντα στην επίλυση πολλών προβλημάτων της τεκτονικής δομής, καθώς και της κινητικής και δυναμικής εικόνας, της αντίστοιχης περιοχής.
Κ. 2.2.7. Σύμβολα και συμβολισμοί για την κατασκευή διαγραμμάτων
Για τη διάκριση των διαφόρων στοιχείων (s-, ss-επιφάνειες, γραμμώσεις, ρηξιγενείς επιφάνειες κλπ), που απεικονίζονται στα διαγράμματα Schmidt, έχουν προταθεί ορισμένοι τρόποι αναπαράστασης, καθ' ενός από αυτά.
Σύμφωνα με την υπάρχουσα διεθνή βιβλιογραφία, δίνουμε τον παρακάτω πίνακα συμβόλων και συμβολισμών, που χρησιμοποιούνται στα διαγράμματα Schmidt (C.T.H. 4, 1969).
|
|